已知二次函數y=-x2+bx+c（b,c為常數）的圖象經過點（1，-2）．
（1）用含有b的代數式表示c；
（2）設該二次函數圖象的頂點坐標是（m,n），當b的值變化時，頂點坐標也隨之變化，求n關于m的函數解析式；
（3）若該二次函數的圖象不經過第二象限，當-2≤x≤4時，函數的最大值與最小值之差為16，求b的值．
【考點】二次函數綜合題．
【答案】（1）c=-b-1．
（2）n=m2-2m-1．
（3）b=0或b=4．
（2）n=m2-2m-1．
（3）b=0或b=4．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：306引用：1難度：0.3
相似題
-
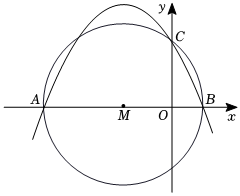1．如圖，拋物線y=-x2-14x+c與x軸相交于點A，B（點A在點B的左側），與y軸相交于點C，點B的坐標為（2，0），⊙M經過A，B，C三點，且圓心M在x軸上．32
（1）求c的值．
（2）求⊙M的半徑．
（3）過點C作直線CD，交x軸于點D，當直線CD與拋物線只有一個交點時直線CD是否與⊙M相切？若相切，請證明；若不相切，請求出直線CD與⊙M的另外一個交點的坐標．發布：2025/6/2 1:30:2組卷：257引用：3難度：0.4 -
2．拋物線y=ax2+bx+c的頂點P的縱坐標為a+b+c.
（1）求a,b應滿足的數量關系；
（2）若拋物線上任意不同兩點A（x1，y1），B（x2，y2）都滿足：當時，（x1-x2）（y1-y2）＜0；當x1＜x2＜ca時，（x1-x2）（y1-y2）＞0．直線y=c與拋物線交于M、N兩點，且△PMN為等腰直角三角形．ca＜x1＜x2
①求拋物線的解析式；
②若直線AB恒過定點（1，1），且以AB為直徑的圓與直線y=m總有公共點，求m的取值范圍．發布：2025/6/2 1:30:2組卷：84引用：1難度：0.1 -
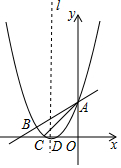3．如圖，已知拋物線y=x2+bx+c與直線y=12x+3交于A，B兩點，交x軸于C、D兩點，連接AC、BC，已知A（0，3），C（-3，0）．12
（1）求此拋物線的解析式；
（2）在拋物線對稱軸l上找一點M，使|MB-MD|的值最大，并求出這個最大值；
（3）點P為y軸右側拋物線上一動點，連接PA，過點P作PQ⊥PA交y軸于點Q，問：是否存在點P，使得以A，P，Q為頂點的三角形與△ABC相似？若存在，請求出所有符合條件的點P的坐標；若不存在，請說明理由．發布：2025/6/2 1:30:2組卷：2880引用：8難度：0.1