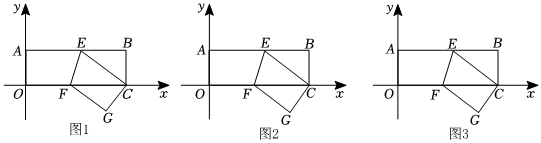
如圖，在平面直角坐標系中，矩形ABCO的頂點O與坐標原點重合，頂點A、C在坐標軸上，B（18，6），將矩形沿EF折疊，使點A與點C點重合．
（1）求點E的坐標；
（2）點P從O出發，沿折線O-A-E方向以每秒2個單位的速度勻速運動，到達終點E時停止運動，設P的運動時間為t,△PCE的面積為S，求S與t的關系式；
（3）在（2）的條件下，當PA=32PE時，在平面直角坐標系中是否存在點Q，使四邊形PEGQ為平行四邊形，若不存在，請說明理由；若存在，請求出點Q的坐標．
PA
=
3
2
PE
【考點】四邊形綜合題．
【答案】（1）E（10，6）；（2）S=
；（3）Q（10.4，-4.8）或（18.4，-4.8）或（5.6，16.8）．
- 8 t + 54 （ 0 ≤ t ≤ 3 ） |
- 6 t + 48 （ 3 ＜ t ≤ 8 ） |
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：30引用：1難度：0.3
相似題
-
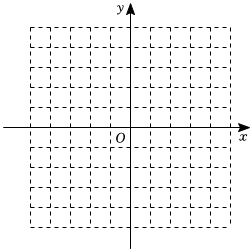1．在如圖所示的直角坐標系中，解答下列問題：
（1）已知A（2，0），B（-1，-4），C（3，-3）三點，分別在坐標系中找出它們，并連接得到△ABC；
（2）將△ABC向上平移4個單位，得到△A1B1C1；
（3）求四邊形A1B1BA的面積．發布：2025/6/5 6:30:2組卷：16引用：4難度：0.5 -
2．閱讀與理解：連接三角形的頂點和它所對的邊的中點所得的線段稱為三角形的中線．
由三角形的中線得出結論：三角形的中線等分三角形的面積．
即如圖1，AD是△ABC中BC邊上的中線，則S△ABD=S△ACD=，12S△ABC
理由：∵BD=CD，∴S△ABD=，即：等底同高的三角形面積相等．12BD×AH=12CD×AH=S△ACD=12S△ABC
操作與探索：在如圖2至圖4中，△ABC的面積為a.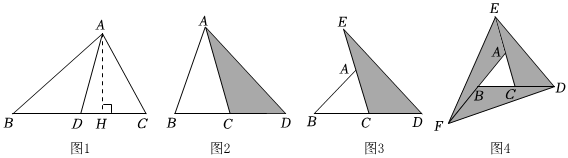
?
（1）如圖2，延長△ABC的邊BC到點D，使CD=BC，連接DA，若△ACD的面積為S1，則S1=（用含a的代數式表示）；
（2）如圖3，延長△ABC的邊BC到點D，延長邊CA到點E，使CD=BC，AE=CA，連接DE，若△DEC的面積為 S2，則S2=（用含a的代數式表示）；
（3）在圖3基礎上延長AB到點F，使BF=AB，連接FD，FE，得到△DEF （如圖4），若陰影部分的面積為S3，則S3=（用含a的代數式表示）．
拓展與應用：如圖5，已知四邊形ABCD的面積是a,E，F，G，H分別是AB，BC，CD，DA的中點，求圖中陰影部分的面積？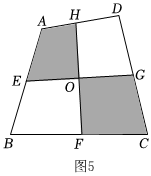
?發布：2025/6/5 6:30:2組卷：265引用：1難度：0.5 -
3．如圖，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，點P從點C出發，以每秒2個單位長度的速度沿CA方向向點A運動，同時，點Q從點B出發，以每秒1個單位長度的速度沿BC方向向點C運動．當一個點到達終點時，另一個點也隨之停止運動．連結PQ，在射線PC上截取PM=PQ，以PQ，PM為鄰邊作菱形PQNM，設運動時間為t秒（t＞0）．
（1）當t=3時，求菱形PQNM的面積．
（2）當△PCQ的面積為菱形PQNM面積的時，求t的值．14
（3）作點B關于直線PQ的對稱點B′．
①當∠BQB'=2∠ABC時，求線段BB'的長．
②當點B′落在菱形PQNM的邊上時，請直接寫出的值．CQBB′
發布：2025/6/5 6:30:2組卷：366引用：4難度：0.3