閱讀與理解：連接三角形的頂點和它所對的邊的中點所得的線段稱為三角形的中線．
由三角形的中線得出結論：三角形的中線等分三角形的面積．
即如圖1，AD是△ABC中BC邊上的中線，則S△ABD=S△ACD=12S△ABC，
理由：∵BD=CD，∴S△ABD=12BD×AH=12CD×AH=S△ACD=12S△ABC，即：等底同高的三角形面積相等．
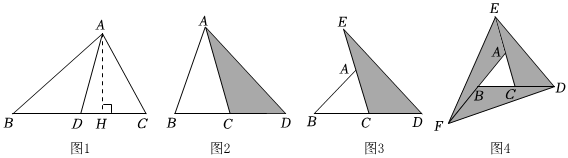
操作與探索：在如圖2至圖4中，△ABC的面積為a.
?
（1）如圖2，延長△ABC的邊BC到點D，使CD=BC，連接DA，若△ACD的面積為S1，則S1=aa（用含a的代數式表示）；
（2）如圖3，延長△ABC的邊BC到點D，延長邊CA到點E，使CD=BC，AE=CA，連接DE，若△DEC的面積為 S2，則S2=2a2a（用含a的代數式表示）；
（3）在圖3基礎上延長AB到點F，使BF=AB，連接FD，FE，得到△DEF （如圖4），若陰影部分的面積為S3，則S3=6a6a（用含a的代數式表示）．
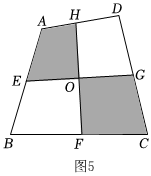
拓展與應用：如圖5，已知四邊形ABCD的面積是a,E，F，G，H分別是AB，BC，CD，DA的中點，求圖中陰影部分的面積？
?
1
2
S
△
ABC
1
2
BD
×
AH
=
1
2
CD
×
AH
=
S
△
ACD
=
1
2
S
△
ABC
【考點】四邊形綜合題．
【答案】a；2a；6a
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/5 6:30:2組卷：267引用：1難度：0.5
相似題
-
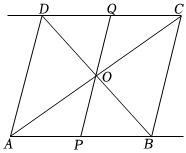1．如圖，在菱形ABCD中，AB=5cm,對角線AC、BD交于點O，且BD=6cm,動點P從點A出發，以1cm/s的速度沿射線AB勻速運動，連接PO并延長，交射線CD于點Q，設點P的運動時間為t（s）．
（1）求AC的長；
（2）當點P在邊AB上時，求四邊形PBCQ的面積；
（3）當點P、Q與菱形ABCD的任意兩個頂點所構成的四邊形是矩形時，求BP的長；
（4）點E是平面內一點，當以點A、P、O、E為頂點的四邊形是菱形時，直接寫出t的值．發布：2025/6/6 18:30:1組卷：68引用：2難度：0.4 -
2．如圖，在正方形ABCD中，E、F是直線DC、CB上的點，且DE=CF，
（1）如圖1，當E、F分別在DC、CB邊上時，連接AE和DF交于點P，請你寫出AE與DF的關系（位置關系和數量關系），并說明理由．
（2）如圖2，當E、F分別在DC、CB的延長線上時，連接AE和DF，（1）中的結論還成立嗎？（請直接回答“是”或“否”，不需證明）
（3）如圖3，當E、F分別在CD、BC的延長線上時，連接AE和DF，（1）中的結論還成立嗎？請說明理由．
發布：2025/6/6 18:30:1組卷：181引用：3難度：0.3 -
3．如圖1，正方形ABCD的邊長為6cm,點F從點B出發，沿射線方向以1cm/秒的速度移動，點E從點D出發，向點A以1cm/秒的速度移動（不到點A）．設點E，F同時出發移動t秒．
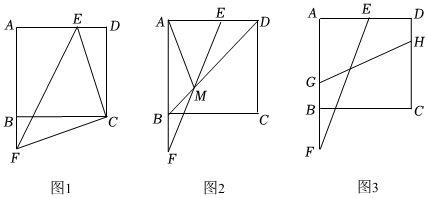
（1）在點E，F移動過程中，連接CE，CF，EF，請判斷△CEF的形狀并說明理由；
（2）如圖2，連接EF，設EF交BD于點M，當t=2時，求AM的長；
（3）如圖3，點G，H分別在邊AB，CD上，且GH=3cm,連接EF，當EF與GH的夾角為45°，求t的值．5發布：2025/6/6 19:0:1組卷：183引用：4難度：0.4