《九章算術》是我國古代內容極為豐富的數學名著，書中有下列問題：“今有勾八步，股十五步，問勾中容圓徑幾何？”其意思是：“今有直角三角形，勾（短直角邊）長為8步，股（長直角邊）長為15步，問該直角三角形能容納的圓（內切圓）的直徑是多少？”你的答案是（ ）
【考點】三角形的內切圓與內心．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/14 21:30:2組卷：62引用：1難度：0.5
相似題
-
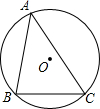1．如圖，半徑為2的⊙O中，弦BC=2，A是優弧BC上的一個動點，P點是△ABC的內心，經過B、C、P三點作⊙M，當點A運動時，⊙M的半徑（ ）3發布：2025/6/15 11:30:1組卷：133引用：1難度：0.9 -
2．△ABC的內切圓O與BC、CA、AB分別相切于點D、E、F，且AB=9，BC=14，CA=13，則AF、BD、CE的長依次為（ ）
發布：2025/6/15 14:0:2組卷：118引用：3難度：0.9 -
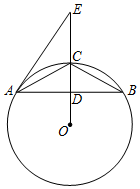3．如圖，⊙O為△ABC的外接圓，D為OC與AB的交點，E為線段OC延長線上一點，且∠EAC=∠ABC．
（1）求證：直線AE是⊙O的切線．
（2）若D為AB的中點，CD=6，AB=16
①求⊙O的半徑；
②求△ABC的內心到點O的距離．發布：2025/6/15 12:30:1組卷：3693引用：6難度：0.1