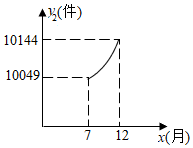
某工廠進(jìn)行加工生產(chǎn)所的工料兩種供應(yīng)方式，一種是從市場上直接采購工料，另一種是通過工廠自身生產(chǎn)工料，該工廠去年（2月至12月）每月所需的工料總量均為12000件，由于工廠生產(chǎn)車間處于調(diào)試階段，自身生產(chǎn)的工料有限，于是工廠從市場上采購一部分工料作為補充，兩種供應(yīng)方式同時進(jìn)行，2月至6月，該工廠從市場上采購的工料量y1（件）與月份x（2≤x≤6，且×為整數(shù)）之間滿足的函數(shù)關(guān)系如表：
| 月份x（月） | 2 | 3 | 4 | 5 | 6 |
| 市場采購工料量y1（噸） | 6000 | 4000 | 3000 | 2400 | 2000 |
1
2
3
4
1
12
（1）請觀察題中的表格和圖象，用所學(xué)過的一次函數(shù)、反比例函數(shù)或二次函數(shù)的有關(guān)知識，分別直接寫出y1，y2與x之間的函數(shù)關(guān)系式；
（2）請你求出該工廠去年（2月至12月）哪個月份所需的工料總費用W（元）最多，并求出這個最多費用．
【考點】二次函數(shù)的應(yīng)用．
【答案】（1）y1=（2≤x≤6，且x取整數(shù)），y2=x2+10000（7≤x≤12，且x取整數(shù)）；（2）去年5月用于所需的工料總費用最多，最多費用是22000元．
12000
x
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：169引用：3難度：0.6
相似題
-
1．【綜合實踐】
某公園在人工湖里安裝一個噴泉，在湖心處豎直安裝一根水管，在水管的頂端安一個噴水頭，噴出的水柱形狀可以看作是拋物線的一部分．若記水柱上某一位置與水管的水平距離為x米，與湖面的垂直高度為y米．下面的表中記錄了x與y的五組數(shù)據(jù)：
（1）在下面網(wǎng)格（圖1）中建立適當(dāng)?shù)钠矫嬷苯亲鴺?biāo)系，并根據(jù)表中所給數(shù)據(jù)畫出表示y與x函數(shù)關(guān)系的圖象；x（米） 0 1 2 3 4 y（米） 0.5 1.25 1.5 1.25 0.5 
（2）若水柱最高點距離湖面的高度為m米，則m=，并求y與x函數(shù)表達(dá)式；
（3）現(xiàn)公園想通過噴泉設(shè)立新的游玩項目，準(zhǔn)備通過只調(diào)節(jié)水管露出湖面的高度，使得游船能從拋物線形水柱下方通過，如圖2所示，為避免游船被噴泉淋到，要求游船從拋物線形水柱下方中間通過時，頂棚上任意一點到水柱的豎直距離均不小于0.5米，已知游船頂棚寬度為3米，頂棚到湖面的高度為2米，那么公園應(yīng)將水管露出湖面的高度（噴水頭忽略不計）至少調(diào)節(jié)到多少米才能符合要求？請通過計算說明理由（結(jié)果保留一位小數(shù)）．發(fā)布：2025/5/23 16:30:1組卷：1253引用：4難度：0.5 -
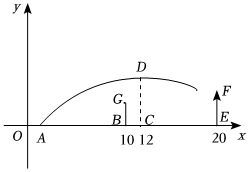2．在某場足球比賽中，球員甲將在地面上點A處的足球?qū)χ蜷T踢出，圖中的拋物線是足球的高度y（m）與球和點O的水平距離x（m）的函數(shù)y=a（x-h）2+k的部分圖象（不考慮空氣的阻力），當(dāng)足球運行到最高點D時，此時球恰好在球員乙的正上方，球員乙在距點O12m的點C處，球距地面的高度為5m,即CD=5m,對方球門與點O的水平距離為20m.
（1）當(dāng)OA=2時，
①求y與x的關(guān)系式；
②當(dāng)球的高度為3.2m時，求足球與對方球門的水平距離；
（2）防守隊員丙站在距點O正前方10m的點B處，球員甲罰出的任意球高過球員丙的頭頂并直接射進(jìn)對方球門，已知丙的身高為1.76m,即BG=1.76m,球門的高度為2.44m,即EF=2.44m,直接寫出a的取值范圍．發(fā)布：2025/5/23 17:0:1組卷：583引用：3難度：0.4 -
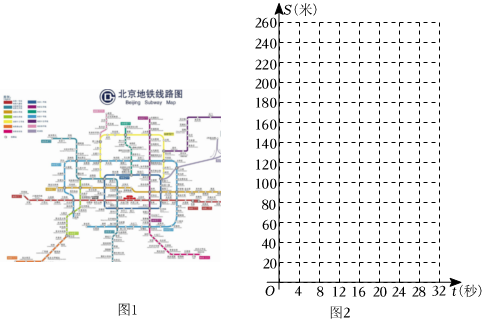
3．“城市軌道交通是現(xiàn)代大城市交通的發(fā)展方向，發(fā)展軌道交通是解決大城市病的有效途徑．”如圖1，北京地鐵（BeijingSubway）是中華人民共和國北京市的城市軌道交通系統(tǒng)，規(guī)劃于1953年，始建于1965年，運營于1969年，是中國第一個地鐵系統(tǒng)．小華了解到列車從慈壽寺站開往花園橋站時，在距離停車線256米處開始減速．他想知道列車從減速開始，經(jīng)過多少秒停下來，以及最后一秒滑行的距離．為了解決這個問題，小華通過建立函數(shù)模型來描述列車離停車線的距離s（米）與滑行時間t（秒）的函數(shù)關(guān)系，再應(yīng)用該函數(shù)解決相應(yīng)的問題．
（1）建立模型
①收集數(shù)據(jù)
②建立平面直角坐標(biāo)系r（秒） 0 4 8 12 16 20 24 … s（米） 256 196 144 100 64 36 16 …
為了觀察s（米）與t（秒）的關(guān)系，建立如圖2所示的平面直角坐標(biāo)系．
③描點連線
請在平面直角坐標(biāo)系中將表中未描出的點補充完整，并用平滑的曲線依次連接．
④選擇函數(shù)模型
觀察這條曲線的形狀，它可能是 函數(shù)的圖象．
⑤求函數(shù)解析式
解：設(shè)s=at2+bt+c（a≠0），因為t=0時，s=256，所以c=256，則s=at2+bt+256．
請根據(jù)表格中的數(shù)據(jù)，求a,b的值．
驗證：把a,b的值代入s=at2+bt+256中，并將其余幾對值代入求出的解析式，發(fā)現(xiàn)它們都滿足該函數(shù)解析式．
（2）應(yīng)用模型
列車從減速開始經(jīng)過 秒，列車停止；最后一秒鐘，列車滑行的距離為 米．發(fā)布：2025/5/23 17:0:1組卷：822引用：5難度：0.4
相關(guān)試卷