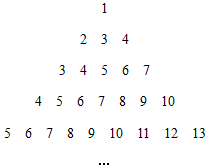將正整數按如圖方式進行有規律的排列，第2行最后一個數是4，第3行最后一個數是7，第4行最后一個數是10，…．按此規律，若2022是第m行第n個數，則m,n的值分別是（ ）
【考點】規律型：數字的變化類．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 12:0:1組卷：520引用：2難度：0.6
相似題
-
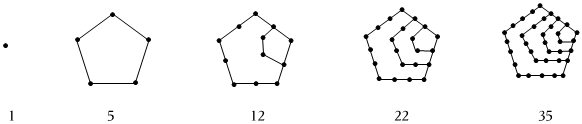
1．法國數學家柯西于1813年在拉格朗日、高斯的基礎上徹底證明了《費馬多邊形數定理》，其主要突破在“五邊形數（點的個數）”的證明上．如圖，這是前幾個“五邊形數”的對應圖形，請據此推斷，第8個“五邊形數”為 ．
發布：2025/6/4 18:30:2組卷：38引用：1難度：0.5 -
2．觀察下面的算式：1×3+1=4=22；2×4+1=9=32；3×5+1=16=42；4×6+1=25=52；…．
?（1）請你寫出2個與上述算式具有相同規律的算式；
（2）用字母表示數，寫出上述算式反映的規律，并加以證明．發布：2025/6/5 5:30:2組卷：32引用：1難度：0.7 -
3．已知x≠1．觀察下列等式：
（1-x）（1+x）=1-x2；
（1-x）（1+x+x2）=1-x3；
（1-x）（1+x+x2+x3）=1-x4；
…
（1）猜想：（1-x）（1+x+x2+x3?+xn-1）=；
（2）應用：根據你的猜想請你計算下列式子的值：
①（1-2）（1+2+22+23+24+25）=；
②（x-1）（x2022+x2021+x2020+…+x2+x+1）=．
（3）求2100+299+298+…+22+2+1的值是多少？發布：2025/6/5 5:30:2組卷：157引用：1難度：0.6