如下是華師版八年級下冊數(shù)學教材117頁的部分內容．
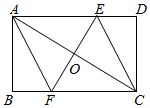
已知：如圖，已知矩形ABCD的對角線AC的垂直平分線與邊AD、BC分別交于點E、F，求證：四邊形AFCE是菱形．
【問題解決】請結合圖①寫出證明過程．
【應用拓展】
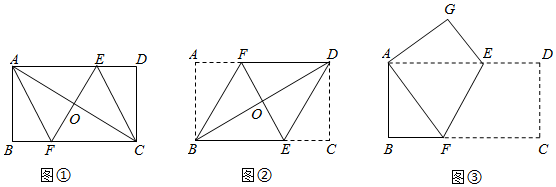
（1）如圖②，矩形紙片ABCD，翻折∠A和∠C，使AB和CD落在對角線BD上，且點A和點C落在同一點O上，折痕分別是BF和DE，若四邊形BEDF面積為8，則矩形紙片ABCD的面積為 1212．
（2）如圖③，矩形紙片ABCD沿著EF折疊，使得點C與點A重合，若AB=4，BC=8，則EF=2525．
5
5
【考點】四邊形綜合題．
【答案】12；2
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：494引用：3難度：0.7
相似題
-
1．如圖，點O為矩形ABCD的對稱中心，AB=10cm,BC=12cm.點E，F(xiàn)，G分別從A，B，C三點同時出發(fā)，沿矩形的邊按逆時針方向勻速運動，點E的運動速度為1cm/s,點F的運動速度為3cm/s,點G的運動速度為xcm/s.當點F到達點C（即點F與點C重合）時，三個點隨之停止運動．在運動過程中，△EBF關于直線EF的對稱圖形是△EB'F，設點E，F(xiàn)，G運動的時間為t（單位：s）．
（1）當t=s時，四邊形EBFB'為正方形；
（2）當x為何值時，以點E，B，F(xiàn)為頂點的三角形與以點F，C，G為頂點的三角形可能全等？
（3）是否存在實數(shù)t,使得點B'與點O重合？若存在，求出t的值；若不存在，請說明理由．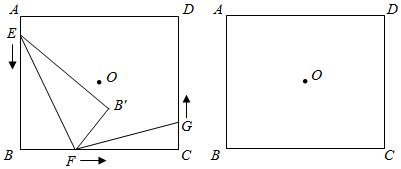
發(fā)布：2025/6/4 10:0:1組卷：1184引用：5難度：0.1 -
2．2023年3月24日，第17屆歐洲杯預選賽正式打響，本屆歐洲杯足球場采用了幾種噴灌系統(tǒng)，如圖1是噴灌系統(tǒng)可以360°旋轉的噴嘴工作實景圖，已知足球場可以近似看成長為96米，寬為64米的矩形．
某實驗室為進一步研究噴灌技術，按比例尺1：8制作了一個足球場沙盤矩形ABCD，如圖2．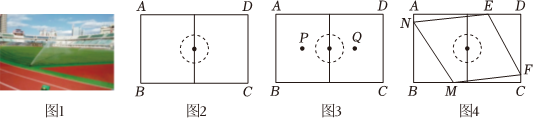
（1）AB=米，BC=米；
（2）如圖3，在足球場沙盤左右半場的兩個中心位置分別安裝一個覆蓋半徑為4.95米的噴嘴P、Q，請問兩個噴嘴同時工作時，能否覆蓋整個足球場沙盤？請說明理由；
（3）如圖4，在足球場沙盤中裝有一個可以平行移動的噴灌桿，初始位置為MN，噴灌桿平移噴灌時覆蓋范圍呈菱形區(qū)域MNEF，M、N、E、F在沙盤邊界上，已知BM=4米，求MN的長；
（4）利用無人機沿著足球場沙盤的對稱軸或對角線飛行并進行左右對稱噴灌，噴灌覆蓋范圍呈正方形，當無人機恰好能噴灌整個足球場沙盤時，請在上述規(guī)定的飛行路線中，任意選擇其中的兩條路線，直接寫出無人機噴灌面積的最小值分別是 平方米（面積相同算同一種）．發(fā)布：2025/6/4 10:0:1組卷：255引用：5難度：0.3 -
3．動態(tài)幾何問題是由點動、線動、形動而構成的，需要用運動與變化的眼光去觀察和研究圖形．有時借助特殊的四邊形常常能幫助我們化“動”為“靜”．
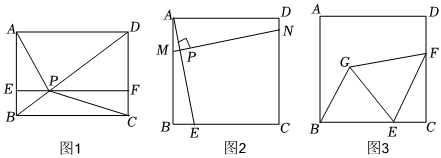
（1）問題1：如圖1，點P為矩形ABCD對角線BD上一動點，過點P作EF∥BC，分別交AB，CD于點E，F(xiàn)．若△AEP的面積為S1，△CFP的面積為S2，則S1與S2的數(shù)量關系是S1S2（填“＞”、“＜”或“=”）；
（2）問題2：如圖2，在正方形ABCD中，E為邊BC上一動點（不與點B、C重合），垂直于AE的一條直線MN分別交AB、AE、CD于點M、P、N．判斷線段DN、MB、EC之間的數(shù)量關系，并說明理由．
（3）問題3：如圖3，正方形ABCD的邊長為4，E為BC上一點，且BE=3，F(xiàn)為CD邊上的一個動點，連接EF，以EF為邊向左側作等邊△EFG，連接BG，則BG的最小值為 ．發(fā)布：2025/6/4 10:0:1組卷：468引用：5難度：0.4