閱讀以下材料,并按要求完成相應的任務:
萊昂哈德?歐拉(LeonhardEuler)是瑞士數學家,在數學上經常見到以他的名字命名的重要常數,公式和定理,下面就是歐拉發現的一個定理:在△ABC中,R和r分別為外接圓和內切圓的半徑,O和I分別為其中外心和內心,則OI2=R2-2Rr.

如圖1,⊙O和⊙I分別是△ABC的外接圓和內切圓,⊙I與AB相切分于點F,設⊙O的半徑為R,⊙I的半徑為r,外心O(三角形三邊垂直平分線的交點)與內心I(三角形三條角平分線的交點)之間的距離OI=d,則有d2=R2-2Rr.
下面是該定理的證明過程(部分):
延長AI交⊙O于點D,過點I作⊙O的直徑MN,連接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所對的圓周角相等).
∴△MDI∽△ANI.
∴IMIA=IDIN,
∴IA?ID=IM?IN,①
如圖2,在圖1(隱去MD,AN)的基礎上作⊙O的直徑DE,
如圖2,動手連接BE,BD,BI,IF.
∵DE是⊙O的直徑,所以∠DBE=90°.
∵⊙I與AB相切于點F,所以∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所對的圓周角相等),
∴△AIF∽△EDB,
∴IADE=IFBD.
∴IA?BD=DE?IF②
(1)觀察發現:IM=R+dR+d,IN=R-dR-d(用含R,d的代數式表示);
(2)請觀察式子①和式子②,并利用任務(1)的結論,按照上面的證明思路,完成該定理證明的剩余部分.
IM
IA
ID
IN
IA
DE
IF
BD
【考點】圓的綜合題.
【答案】R+d;R-d
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:86引用:1難度:0.4
相似題
-
1.【教材呈現】以下是浙教版八年級下冊數學教材第85頁的部分內容.
先觀察圖,直線l1∥l2,點A,B在直線l2上,點C1,C2,C3,C4在直線l1上.△ABC1,△ABC2,△ABC3,△ABC4這些三角形的面積有怎樣的關系?請說明理由.
【基礎鞏固】如圖1,正方形ABCD內接于⊙O,直徑MN∥AD,求陰影面積與圓面積的比值;
【嘗試應用】如圖2,在半徑為5的⊙O中,BD=CD,∠ACO=2∠BDO,cos∠BOC=x,用含x的代數式表示S△ABC
;
【拓展提高】如圖3,AB是⊙O的直徑,點P是OB上一點,過點P作弦CD⊥AB于點P,點F是⊙O上的點,且滿足CF=CB,連接BF交CD于點E,若BF=8EP,S△CEF=10,求⊙O的半徑.2 ?發布:2025/5/22 7:0:2組卷:542引用:2難度:0.1
?發布:2025/5/22 7:0:2組卷:542引用:2難度:0.1 -
2.如圖,直線y=-2x+10與x軸交于點A,與y軸交于點B,以OB為直徑的⊙M交AB于另一點C,點D在⊙M上.分別過點O,B作直線CD的垂線段,垂足為E,F,連結OC.
(1)求點A,B,C的坐標.
(2)當點D在直線BC右側時,
①求證:EC?CF=OE?BF;
②求證:EC=DF.
(3)CD與EF的距離和是否為定值?若是,請直接寫出定值;若不是,請直接寫出取到最小值時直線CD的解析式.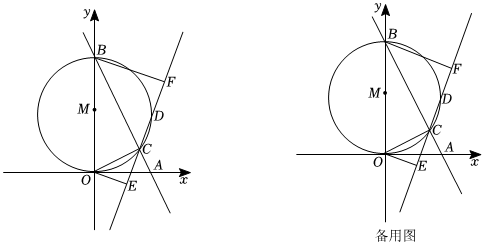 發布:2025/5/22 7:0:2組卷:172引用:1難度:0.4
發布:2025/5/22 7:0:2組卷:172引用:1難度:0.4 -
 3.已知:點P為圖形M上任意一點,點Q為圖形N上任意一點,若點P與點Q之間的距離PQ始終滿足PQ>0,則稱圖形M與圖形N相離.
3.已知:點P為圖形M上任意一點,點Q為圖形N上任意一點,若點P與點Q之間的距離PQ始終滿足PQ>0,則稱圖形M與圖形N相離.
(1)已知點A(1,2)、B(0,-5)、C(2,-1)、D(3,4).
①與直線y=3x-5相離的點是;
②若直線y=3x+b與△ABC相離,求b的取值范圍;
(2)設直線y=x+3、直線y=-3x+3及直線y=-2圍成的圖形為W,⊙T的半徑為1,圓心T的坐標為(t,0),直接寫出⊙T與圖形W相離的t的取值范圍.3發布:2025/5/22 7:0:2組卷:421引用:3難度:0.3


