已知在數軸上，從左往右依次有四個點A，C，D，B，其中點A，B對應的數分別為-7和9．
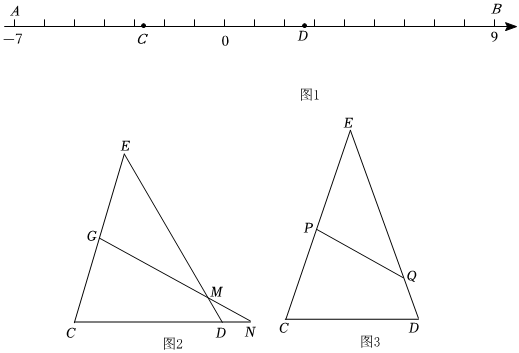
（1）利用直尺和圓規作圖：如圖1，已知線段AC，CD，DB，在數軸上方，求作△ECD，使得EC=AC，ED=BD（只保留作圖痕跡）；
?（2）在（1）的條件下，在數軸上找一點F，直接作出直線EF，使得直線EF平分△ECD的周長；
（3）如圖2，在△ECD中，點G為CE中點，過點G的直線交ED于M，交CD的延長線于N，若DM=DN，求證：直線GN平分△ECD的周長；
（4）如圖3，若EC=ED，點P在邊CE上，點Q在邊ED上，且PQ平分△ECD的周長．
請問線段PQ的長是否為定值？若是定值，請說明理由；若不是定值，當EP與EQ滿足什么關系時，線段PQ最短，并說明理由．
?
【考點】三角形綜合題．
【答案】（1）圖見解析；
（2）圖見解析；
（3）證明見解析；
（4）EP=EQ時，PQ最短．
（2）圖見解析；
（3）證明見解析；
（4）EP=EQ時，PQ最短．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 22:30:1組卷：85引用：2難度：0.2
相似題
-
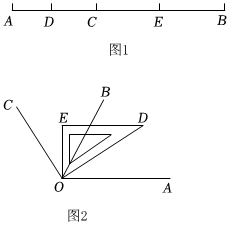1．線段和角是我們初中數學常見的平面幾何圖形，它們的表示方法、和差計算以及線段的中點、角的平分線的概念等有很多相似之處，所以研究線段或角的問題時可以運用類比的方法．
（1）特例感知：
如圖1，已知AB=10cm,點D是線段AC的中點，點E是線段BC的中點．若BC=6cm,則線段DE=cm.
（2）數學思考：
如圖1，已知AB=10cm,若C是線段AB上的一個動點，點D是線段AC的中點，點E是線段BC的中點，線段DE的長會發生變化嗎？說明理由．
（3）知識遷移：
如圖2，OB是∠AOC內部的一條射線，把三角尺中60°角的頂點放在點O處，轉動三角尺，當三角尺的邊OD平分∠AOB時，在角尺的另一邊OE與正好平分∠BOC，求∠AOC的度數．發布：2025/6/5 16:30:2組卷：126引用：1難度：0.6 -
2．在平面直角坐標系中，A（6，a），B（b,0），M（0，c），且
，P點為y軸上一動點．（b-2）2+|a-6|+c-6=0
（1）求點B、M的坐標；
（2）當P點在線段OM上運動時，試問是否存在一個點P使S△PAB=13，若存在，請求出P點的坐標；若不存在，請說明理由．
（3）不論點P點運動到直線OM上的任何位置（不包括點O，M），∠PAM、∠APB、∠PBO三者之間是否都存在某種固定的數量關系，如果有，請寫出來并請選擇其中一種結論進行證明；如果沒有，請說明理由．發布：2025/6/5 18:0:1組卷：35引用：3難度：0.1 -
3．在△ABC中，∠BAC=90°，
，D為BC上任意一點，E為AC上任意一點．AB=AC=22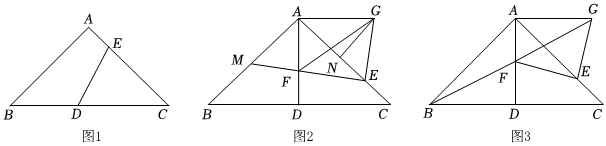
（1）如圖1，連接DE，若∠CDE=60°，AC=4AE，求DE的長．
（2）如圖2，若點D為BC中點，連接AD，點F為AD上任意一點，連接EF并延長交AB于點M，將線段EF繞點E順時針旋轉90°得到線段EG，連接AG．點N在AC上，∠AGN=∠AEG且，求證：GN=MF．AM+AF=2AE
（3）如圖3，點D為BC中點，連接AD，點F為AD的中點，連接EF、BF，將線段EF繞點E順時針旋轉90°得到線段EG，連接AG，H為直線AB上一動點，連接FH，將△BFH沿FH翻折至△ABC所在平面內，得到△B′FH，連接B′G，直接寫出線段B′G的長度的最大值．發布：2025/6/5 18:0:1組卷：415引用：2難度：0.1