在△ABC中，∠BAC=90°，AB=AC=22，D為BC上任意一點，E為AC上任意一點．
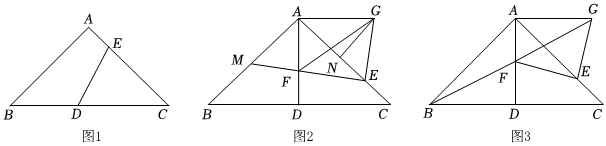
（1）如圖1，連接DE，若∠CDE=60°，AC=4AE，求DE的長．
（2）如圖2，若點D為BC中點，連接AD，點F為AD上任意一點，連接EF并延長交AB于點M，將線段EF繞點E順時針旋轉90°得到線段EG，連接AG．點N在AC上，∠AGN=∠AEG且AM+AF=2AE，求證：GN=MF．
（3）如圖3，點D為BC中點，連接AD，點F為AD的中點，連接EF、BF，將線段EF繞點E順時針旋轉90°得到線段EG，連接AG，H為直線AB上一動點，連接FH，將△BFH沿FH翻折至△ABC所在平面內，得到△B′FH，連接B′G，直接寫出線段B′G的長度的最大值．
AB
=
AC
=
2
2
AM
+
AF
=
2
AE
【考點】三角形綜合題．
【答案】（1）；
（2）證明見解析部分；
（3）+．
3
（2）證明見解析部分；
（3）
5
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/5 18:0:1組卷：415引用：2難度：0.1
相似題
-
1．已知關于x的一元二次方程（a+c）x2-4bx-4（a-c）=0，其中a,b,c分別為△ABC三邊的長．
（1）如果x=2是方程的根，則△ABC的形狀為 ；
（2）如果方程有兩個相等的實數根，試判斷△ABC的形狀，并說明理由；
（3）如果△ABC是等邊三角形，試求這個一元二次方程的根．發布：2025/6/7 0:0:1組卷：235引用：2難度：0.4 -
2．如圖，在△ABC中，AB=AC=5cm,BC=6cm,BD⊥AC交AC于點D．動點P從點C出發，按C→A→B→C的路徑運動，且速度為4cm/s,設出發時間為t s.
（1）求BC上的高；
（2）當CP⊥AB時，求t的值；
（3）當點P在BC邊上運動時，若△CDP是等腰三角形，求出所有滿足條件的t的值．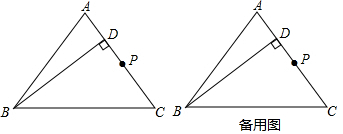
發布：2025/6/7 0:30:1組卷：550引用：5難度：0.1 -
3．如圖，等腰直角△OAB中OA=OB．
（1）過點A作AD⊥OA，線段OA上一點C滿足∠CDB=∠OBD．求∠CBD的度數；
（2）過點B作BE⊥OB，線段OB上一點F滿足∠AFE=60°，∠AEF=75°，過點A作AG⊥BE于點G，試求的值．GE+OFBF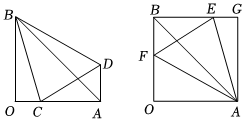
發布：2025/6/7 1:30:1組卷：257引用：1難度：0.3