已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=BC．
（1）如圖1．連接BD，若∠BAD=90°，求證：AD=CD．
（2）如圖2，點P，Q分別在線段AD，DC上，滿足PQ=AP+CQ，求證：∠PBQ=∠ABP+∠QBC；
（3）若點Q在DC的延長線上，點P在DA的延長線上，如圖3所示，仍然滿足PQ=AP+CQ，請寫出∠PBQ與∠ADC的數量關系，并給出證明過程．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 0:0:1組卷：434引用：2難度：0.3
相似題
-
1．閱讀：基本圖形通常是指能夠反映一個或幾個定理，或者能夠反映圖形基本規律的幾何圖形．這些圖形以基本概念、基本事實、定理、常用的數學結論和基本規律為基礎，圖形簡單又具有代表性．在幾何問題中，熟練把握和靈活構造基本圖形，能更好地幫助我們解決問題．
我們將圖1①所示的圖形稱為“8字形”．在這個“8字形”中，存在結論∠A+∠B=∠C+∠D．
我們將圖1②所示的凹四邊形稱為“飛鏢形”．在這個“飛鏢形”中，存在結論∠AOC=∠A+∠C+∠P．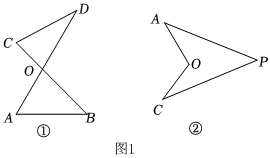
（1）直接利用上述基本圖形中的任意一種，解決問題：
如圖2，AP、CP分別平分∠BAD、∠BCD，說明：∠P=（∠B+∠D）．12
（2）將圖2看作基本圖形，直接利用（1）中的結論解決下列問題：
①如圖3，直線AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠B=30°，∠D=20°，求∠P的度數．
②在圖4中，AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P與∠B、∠D的關系（直接寫出結果，無需說明理由）．
③在圖5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P與∠B、∠D的關系（直接寫出結果，無需說明理由）．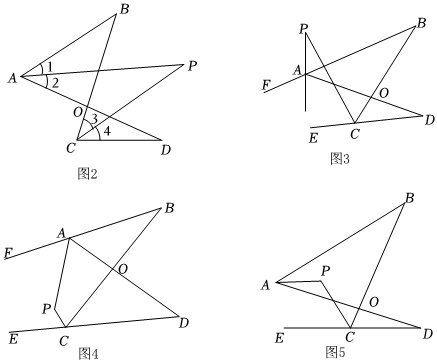
發布：2025/6/4 16:0:1組卷：395引用：3難度：0.1 -
2．如圖1，四邊形ABCD，連接AC，AB=AC=AD．
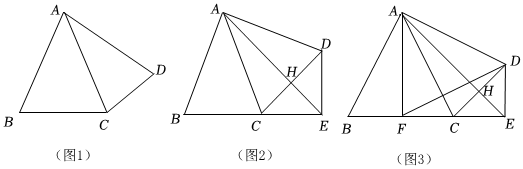
（1）求證：；12∠BAD+∠BCD=180°
（2）如圖2，作∠CAD的平分線交BC的延長線于點E，交CD于點H，連接DE，當∠BAD=90°時，求證：；BC+2DE=2AE
（3）如圖3，在（2）的條件下，過點A作AF⊥BC于F，連接FD，若，△AFD的面積是10，求線段DF的長．AB=5DE發布：2025/6/4 16:0:1組卷：72引用：1難度：0.3 -
3．概念理解
一組對邊平行，另一組對邊相等且不平行的四邊形叫做等腰梯形．
類比研究
我們在學完平行四邊形后，知道可以從對稱性、邊、角和對角線四個角度對四邊形進行研究．請根據示例圖形，完成表．
演繹論證四邊形 示例圖形 對稱性 邊 角 對角線 平行
四邊形（1） ．兩組對邊分別平行，兩組對邊分別相等． 兩組對角
分別相等．對角線互相平分． 等腰
梯形軸對稱圖形，過平行的一組對邊中點的直線是它的對稱軸． 一組對邊平行，另一組對邊相等． （2） ．（3） ．
證明等腰梯形有關角和對角線的性質．
（4）已知：在等腰梯形ABCD中，AD∥BC，AB=DC，AC、BD是對角線．
求證：．
證明：
揭示關系
我們可以用圖來揭示三角形和一些特殊三角形之間的關系．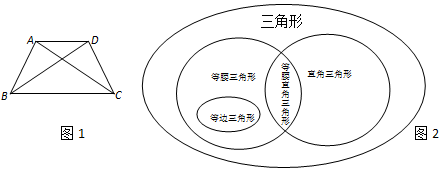
（5）請用類似的方法揭示四邊形、對角線相等的四邊形、平行四邊形、矩形以及等腰梯形之間的關系．發布：2025/6/4 16:0:1組卷：346引用：2難度：0.1