如圖1，四邊形ABCD，連接AC，AB=AC=AD．
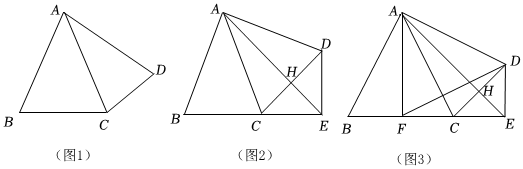
（1）求證：12∠BAD+∠BCD=180°；
（2）如圖2，作∠CAD的平分線交BC的延長(zhǎng)線于點(diǎn)E，交CD于點(diǎn)H，連接DE，當(dāng)∠BAD=90°時(shí)，求證：BC+2DE=2AE；
（3）如圖3，在（2）的條件下，過(guò)點(diǎn)A作AF⊥BC于F，連接FD，若AB=5DE，△AFD的面積是10，求線段DF的長(zhǎng)．
1
2
∠
BAD
+
∠
BCD
=
180
°
BC
+
2
DE
=
2
AE
AB
=
5
DE
【考點(diǎn)】四邊形綜合題．
【答案】（1）證明見(jiàn)解析；
（2）證明見(jiàn)解析；
（3）DF=5．
（2）證明見(jiàn)解析；
（3）DF=5．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/4 16:0:1組卷：72引用：1難度：0.3
相似題
-
1．矩形ABCD中，連接AC，BE⊥AC于E，
（1）如圖1，求證：∠ACD=∠CBE；
（2）如圖2，延長(zhǎng)EB至點(diǎn)F，使BF=AC，連接FD交AB于點(diǎn)M，求證：AD=AM；
（3）如圖3，在（2）的條件下，取DF的中點(diǎn)G，連接AG、AF，∠GFA+2∠AGD=45°，AD=2，求FA的長(zhǎng)．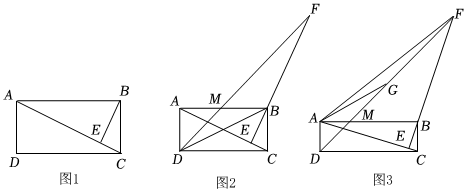
發(fā)布：2025/6/6 9:30:1組卷：14引用：1難度：0.2 -
2．如圖1，在平面直角坐標(biāo)系中，A（a,0）是x軸正半軸上一點(diǎn)，C是第四象限一點(diǎn)，CB⊥y軸，交y軸負(fù)半軸于B（0，b），且
，四邊形AOBC的面積是16．（a-3）2+b+4=0
（1）求C點(diǎn)的坐標(biāo)．
（2）如圖2，設(shè)D為線段OB上一動(dòng)點(diǎn)，當(dāng)AD⊥AC時(shí)，∠ODA的角平分線與∠CAE的角平分線的反向延長(zhǎng)線交于點(diǎn)P，求∠APD的度數(shù)．
（3）如圖3，當(dāng)D點(diǎn)在線段OB上運(yùn)動(dòng)時(shí)，作DM⊥AD交BC于M點(diǎn)，∠BMD、∠DAO的平分線交于N點(diǎn)，則D在運(yùn)動(dòng)過(guò)程中，∠N的大小是否變化？若不變，求出其值，若變化，請(qǐng)說(shuō)明理由．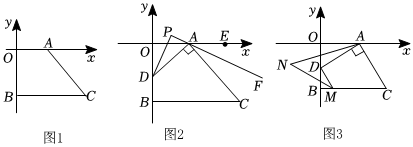
???發(fā)布：2025/6/6 9:30:1組卷：135引用：1難度：0.1 -
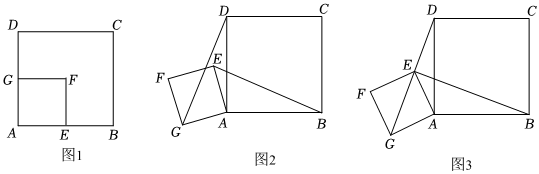
3．已知四邊形ABCD與AEFG均為正方形．
數(shù)學(xué)思考：
（1）如圖1，當(dāng)點(diǎn)E在AB邊上，點(diǎn)G在AD邊上時(shí)，線段BE與DG的數(shù)量關(guān)系是 ，位置關(guān)系是 ．
（2）在圖1的基礎(chǔ)上，將正方形AEFG以點(diǎn)A為旋轉(zhuǎn)中心，逆時(shí)針旋轉(zhuǎn)角度α，得到圖2，則（1）中的結(jié)論是否仍然成立？若成立，請(qǐng)證明；若不成立，請(qǐng)說(shuō)明理由；
拓展探索：
（3）如圖3，若點(diǎn)D，E，G在同一直線上，且AB=2AE=2，則線段BE長(zhǎng)為 ．（直接寫出答案即可，不要求寫過(guò)程）．2發(fā)布：2025/6/6 10:0:1組卷：50引用：2難度：0.6