概念理解
一組對邊平行,另一組對邊相等且不平行的四邊形叫做等腰梯形.
類比研究
我們在學完平行四邊形后,知道可以從對稱性、邊、角和對角線四個角度對四邊形進行研究.請根據示例圖形,完成表.
| 四邊形 | 示例圖形 | 對稱性 | 邊 | 角 | 對角線 |
| 平行 四邊形 | (1) 中心對稱圖形,對角線的交點是它的對稱中心 中心對稱圖形,對角線的交點是它的對稱中心 . | 兩組對邊分別平行,兩組對邊分別相等. | 兩組對角 分別相等. | 對角線互相平分. | |
| 等腰 梯形 | 軸對稱圖形,過平行的一組對邊中點的直線是它的對稱軸. | 一組對邊平行,另一組對邊相等. | (2) 同一底上的兩個角相等 同一底上的兩個角相等 . | (3) 對角線相等 對角線相等 . |
證明等腰梯形有關角和對角線的性質.
(4)已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是對角線.
求證:
∠ABC=∠DCB,∠BAD=∠CDA,AC=BD
∠ABC=∠DCB,∠BAD=∠CDA,AC=BD
.證明:
揭示關系
我們可以用圖來揭示三角形和一些特殊三角形之間的關系.
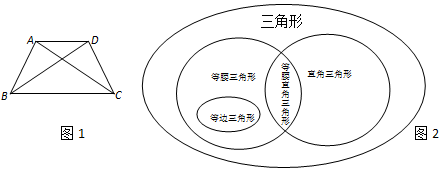
(5)請用類似的方法揭示四邊形、對角線相等的四邊形、平行四邊形、矩形以及等腰梯形之間的關系.
【考點】四邊形綜合題.
【答案】中心對稱圖形,對角線的交點是它的對稱中心;同一底上的兩個角相等;對角線相等;∠ABC=∠DCB,∠BAD=∠CDA,AC=BD
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:346引用:2難度:0.1
相似題
-
1.四邊形ABCD為正方形,邊長為6,點M為對角線BD上一動點(不與點B,D重合),連接CM,過點M作MN⊥CM,交射線AB于點N.
(1)如圖1,求證:MC=MN;
(2)如圖2,作射線CN交射線DB于點P.
①當點N在邊AB上時,設BN的長為x,△CMN的面積為y,求y關于x的函數解析式;
②當BN=3時,請直接寫出MP的長.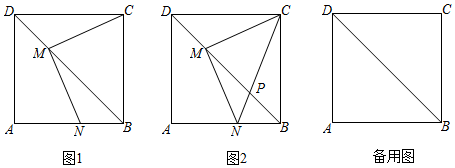 發布:2025/6/2 13:0:2組卷:207引用:4難度:0.2
發布:2025/6/2 13:0:2組卷:207引用:4難度:0.2 -
2.如圖1,在正方形ABCD中,M、N分別為邊AB、AD上的點,連接CM、CN,且CM=CN.
(1)求證:△BMC≌△DNC;
(2)如圖2,若P是邊BC上的點,且NP⊥CM于O,連接OA,求證:OM+ON=OA;2
(3)如圖3,在滿足(2)的條件下,過O作OQ⊥BC于Q,若AM=2BM,求的值.OQCD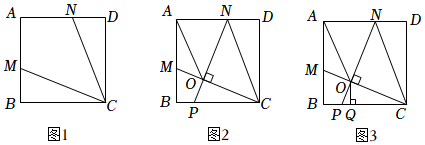 發布:2025/6/2 16:0:1組卷:755引用:4難度:0.4
發布:2025/6/2 16:0:1組卷:755引用:4難度:0.4 -
3.如圖,在平面直角坐標系中,已知矩形OABC的頂點A在x軸上,頂點C在y軸上,OA=8,OC=4,點P為對角線AC上一動點,過點P作PQ⊥PB,PQ交x軸于點Q.
(1)tan∠ACB=;
(2)在點P從點C運動到點A的過程中,的值是否發生變化?如果變化,請求出其變化范圍;如果不變,請求出其值;PQPB
(3)若將△QAB沿直線BQ折疊后,點A與點P重合,求PC的長.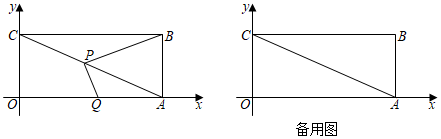 發布:2025/6/2 13:30:2組卷:504引用:2難度:0.4
發布:2025/6/2 13:30:2組卷:504引用:2難度:0.4


