已知2a-b=4，則2a3-a2b+b2-4ab的值為（ ）
【考點】因式分解的應用．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：159引用：1難度：0.7
相似題
-
1．學習《第九章乘法公式與因式分解》時，我們借助拼圖驗證了許多乘法公式，反過來，我們也可以利用拼圖，將一些多項式因式分解，這是研究數學問題的一種常用方法．如圖（1），有足夠多的邊長為a的大正方形，長為a,寬為b的長方形和邊長為b的小正方形．
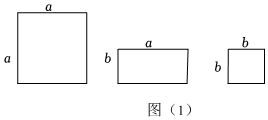
（1）利用拼圖將多項式2a2+5ab+2b2進行因式分解，畫出你的拼圖，并寫出因式分解的結果；
2a2+5ab+2b2=．
（2）若多項式9a2+12ab+kb2（k為正整數）可以用拼圖法因式分解，則k=；
（3）如圖（2），它是由四個形狀、大小完全相同的直角三角形與中間的小正方形EFGH拼成的一個大正方形ABCD．如果每個直角三角形的較短的邊長為a,較長的邊長為b,最長的邊長為c.你能發現直角三角形的三邊長a、b、c的什么數量關系？（注：寫出解答過程）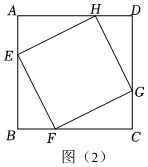
發布：2025/6/13 18:0:2組卷：278引用：2難度：0.5 -
2．閱讀：材料1：只含有一個未知數，并且未知數的最高次數是2次，最高次項的系數不為零，這樣的整式方程叫做一元二次方程．一元二次方程有一種解法是利用因式分解來解的．如解方程：x2-3x+2=0，左邊分解因式得（x-1）（x-2）=0，所以x-1=0或x-2=0，所以原方程的解是x=1或x=2．
材料2：立方和公式用字母表示為：x3+y3=（x+y）（x2-xy+y2），
（1）請利用材料1的方法解方程：x2-4x+3=0；
（2）請根據材料2類比寫出立方差公式：x3-y3=；（提示：可以用換元方法）
（3）結合材料1和2，請你寫出方程x6-7x3-8=0所有根中的兩個根．發布：2025/6/13 6:30:2組卷：1732引用：5難度：0.4 -
3．材料一：已知N為一個四位自然數，若N滿足千位上的數字等于個位上的數字，百位上的數字等于十位和個位上的數字之和，則稱N為“等和數”．
材料二：對于一個“等和數”N，將N的百位數字記為n,千位與百位上的數字之和與十位土的數字的積記為k,令F（N）=3n2+k.
例如：當N=2312時，∵2=2且3=1+2，∴2312是“等和數”：此時，n=3，k=（2+3）×1=5，F（2312）=3×32+5=32；當N=4524時，∵4=4但5≠2+4，∴4524不是“等和數”．
（1）請判斷3543，1211是否是“等和數”，并說明理由；如果是，請求出對應的F（N）的值；
（2）若一個數是某個整數的平方，則稱這個數為完全平方數．已知N是個位上的數字小于十位上的數字的“等和數，將N的各個數位上的數字之和記為G（N），若為完全平方數，求N的所有可能值．F（N）G（N）發布：2025/6/13 12:0:1組卷：273引用：2難度：0.5