(1)按照要求畫出圖形:畫等邊三角形△ABC,點D在BC的延長線上,連接AD,以AD為邊作等邊三角形△ADE,連接CE;
(2)請寫出AC、CD、CE之間的數量關系并證明;
(3)若AB=6cm,點D從點C出發,在BC的延長線上運動,點D的運動速度為每秒2cm,運動時間為t秒,則t為何值時,CE⊥AD?
【考點】三角形綜合題.
【答案】(1)圖形見解答;(2)AC+CD=CE;證明見解答;(3)3.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/2 6:30:2組卷:143引用:2難度:0.3
相似題
-
1.閱讀材料:若m2-2mn+2n2-4n+4=0,求m,n的值,
解:∵m2-2mn+2n2-4n+4=0,
∴(m2-2mn+n2)+(n2-4n+4)=0,
∴(m-n)2+(n-2)2=0,
∵(m-n)2≥0;(n-2)2≥0,
∴(m-n)2=0,(n-2)2=0,
∴n=2,m=2.
根據你的觀察,探究下面的問題:
(1)a2+b2+6a-2b+10=0,則a=,b=;
(2)已知x2+2y2-2xy+8y+16=0,求xy的值;
(3)已知△ABC的三邊長a、b、c都是正整數,且滿足2a2+b2-8a-8b+24=0,求符合條件的△ABC的邊長;當△ABC為等腰三角形時,求三角形的面積.發布:2025/6/3 21:30:1組卷:225引用:2難度:0.2 -
2.綜合實踐
在學習全等三角形的知識時,數學興趣小組發現這樣一個模型:它是由兩個共頂點且頂角相等的等腰三角形構成的,在相對位置變化的同時,始終存在一對全等三角形.興趣小組成員經過研討給出定義:如果兩個等腰三角形的頂角相等,且頂角的頂點互相重合,則稱此圖形為“手拉手全等模型”.因為頂點相連的四條邊,可以形象地看作兩雙手,所以通常稱為“手拉手模型”,如圖1,△ABC與△ADE都是等腰三角形,其中∠BAC=∠DAE,則△ABD≌△ACE(SAS).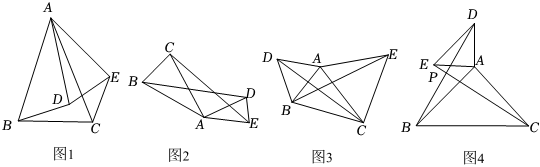
[初步把握]如圖2,△ABC與△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,則有 ≌.
[深入研究]如圖3,已知△ABC,以AB、AC為邊分別向外作等邊△ABD和等邊△ACE,并連接BE,CD,求證:BE=CD.
[拓展延伸]如圖4,在兩個等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,連接BD,CE,交于點P,請判斷BD和CE的關系,并說明理由.發布:2025/6/3 21:30:1組卷:2306引用:11難度:0.3 -
3.閱讀以下材料,完成以下兩個問題.
[閱讀材料]已知:如圖,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,過D作DF∥BA交AE于點F,DF=AC.求證:AE平分∠BAC.
結合此題,DE=EC,點E是DC的中點,考慮倍長,并且要考慮連接哪兩點,目的是證明全等,從而轉移邊和角.有兩種考慮方法:①考慮倍長FE,如圖(1)所示;②考慮倍長AE,如圖(2)所示
以圖(1)為例,證明過程如下:
證明:延長FE至G,使EG=EF,連接CG.
在△DEF和△CEG中,,ED=EC∠DEF=∠CEGEF=EG
∴△DEF≌△CEG(SAS).
∴DF=CG,∠DFE=∠G.
∵DF=AC,
∴CG=AC.
∴∠G=∠CAE.
∴∠DFE=∠CAE.
∵DF∥AB,
∴∠DFE=∠BAE.
∴∠BAE=∠CAE.
∴AE平分∠BAC.
問題1:參考上述方法,請完成圖(2)的證明.
問題2:根據上述材料,完成下列問題:
已知,如圖3,在△ABC中,AD是BC邊上的中線,分別以AB,AC為直角邊向外作等腰直角三角形,∠BAE=∠CAF=90°,AE=AB,AC=AF,AD=3,求EF的長.發布:2025/6/3 20:30:2組卷:2541引用:4難度:0.3


