閱讀材料：若m2-2mn+2n2-4n+4=0，求m,n的值，
解：∵m2-2mn+2n2-4n+4=0，
∴（m2-2mn+n2）+（n2-4n+4）=0，
∴（m-n）2+（n-2）2=0，
∵（m-n）2≥0；（n-2）2≥0，
∴（m-n）2=0，（n-2）2=0，
∴n=2，m=2．
根據(jù)你的觀察，探究下面的問題：
（1）a2+b2+6a-2b+10=0，則a=-3-3，b=11；
（2）已知x2+2y2-2xy+8y+16=0，求xy的值；
（3）已知△ABC的三邊長a、b、c都是正整數(shù)，且滿足2a2+b2-8a-8b+24=0，求符合條件的△ABC的邊長；當△ABC為等腰三角形時，求三角形的面積．
【考點】三角形綜合題．
【答案】-3；1
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/3 21:30:1組卷：225引用：2難度：0.2
相似題
-
1．如圖，△ABC中，∠BAC=90°，以直角邊AC為腰，向外作等腰直角三角形ACD，AC=CD，∠ACD=90°，點E是BC邊上一點，且CE=CD，∠ABC=2∠CED．
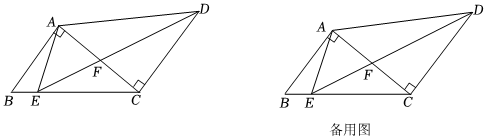
（1）探究：∠CDE與∠ACB的數(shù)量關(guān)系；
（2）求證：BC=CF+AB；
（3）若AD=4，AB=3，求EF的長．2發(fā)布：2025/6/5 12:0:1組卷：417引用：5難度：0.1 -
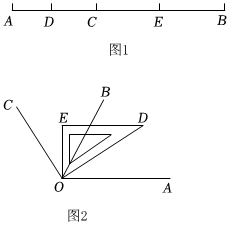2．線段和角是我們初中數(shù)學常見的平面幾何圖形，它們的表示方法、和差計算以及線段的中點、角的平分線的概念等有很多相似之處，所以研究線段或角的問題時可以運用類比的方法．
（1）特例感知：
如圖1，已知AB=10cm,點D是線段AC的中點，點E是線段BC的中點．若BC=6cm,則線段DE=cm.
（2）數(shù)學思考：
如圖1，已知AB=10cm,若C是線段AB上的一個動點，點D是線段AC的中點，點E是線段BC的中點，線段DE的長會發(fā)生變化嗎？說明理由．
（3）知識遷移：
如圖2，OB是∠AOC內(nèi)部的一條射線，把三角尺中60°角的頂點放在點O處，轉(zhuǎn)動三角尺，當三角尺的邊OD平分∠AOB時，在角尺的另一邊OE與正好平分∠BOC，求∠AOC的度數(shù)．發(fā)布：2025/6/5 16:30:2組卷：126引用：1難度：0.6 -
3．如圖，點C為線段AE上一動點（不與點A、E重合），在AE同側(cè)分別作等邊△ABC和等邊△CDE，AD與BE交于點O，AD與BC交于點P，BE與CD交于點Q，連接PQ，以下結(jié)論：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤線段AD繞著點C順時針旋轉(zhuǎn)60度可與線段BE重合；⑥△CPQ為等邊三角形；正確的有 ．（填序號）發(fā)布：2025/6/5 11:30:2組卷：306引用：1難度：0.3