在平面直角坐標系中，二次函數y=-x2+2mx+4-m2的圖象與x軸交于A，B兩點（點A在點B的左側）．
（1）若點B的坐標為（3，0），
①求此時二次函數的解析式；
②當2≤x≤n時，函數值y的取值范圍是-n-1≤y≤3，求n的值；
（2）將該二次函數圖象在x軸上方的部分沿x軸翻折，其他部分保持不變，得到一個新的函數圖象，若當-2＜x≤-1時，這個新函數的函數值y隨x的增大而增大，結合函數圖象，求m的取值范圍．
【答案】（1）①y=-x2+2x+3，②m的取值范圍是-3≤m≤-2或m≥1；（2）m的取值范圍是-3≤m＜-2或m≥1．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/11 8:0:9組卷：402引用：3難度：0.4
相似題
-
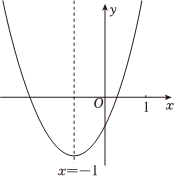1．已知二次函數y=ax2+bx+c（a≠0）圖象的對稱軸為直線x=-1，部分圖象如圖所示，下列結論中：①abc＞0；②b2-4ac＞0；③4a+c＞0；④若t為任意實數，則有a-bt≤at2+b；⑤當圖象經過點（，2）時，方程ax2+bx+c-2=0的兩根為x1，x2（x1＜x2），則x1+2x2=-12，其中正確的結論是（ ）32發布：2025/5/26 3:30:1組卷：740引用：12難度：0.6 -
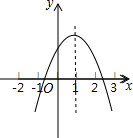2．二次函數y=ax2+bx+c的圖象如圖所示，現有以下結論：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b≥m（am+b）．
其中正確的結論有（ ）發布：2025/5/26 4:0:1組卷：344引用：1難度：0.9 -
3．小明研究二次函數y=（x-m）2+m-1（m為常數）性質時，得出如下結論：①這個函數圖象的頂點始終在直線y=x-1上；②存在兩個m的值，使得函數圖象的頂點與x軸的兩個交點構成等腰直角三角形；③點A（x1，y1）與點B（x2，y2）在函數圖象上，若x1＜x2，x1+x2＞2m,則y1＜y2；④當-1＜x＜3時，y隨x的增大而減小，則m的取值范圍為m≥3．其中錯誤結論的序號是（ ）
發布：2025/5/26 3:0:2組卷：139引用：1難度：0.5