在平面直角坐標系中，已知點A在第一象限，點B在y軸的正半軸上，B0=a,AO=b,AB=c,且有a2+c2+2b2-2ab-2bc=0．
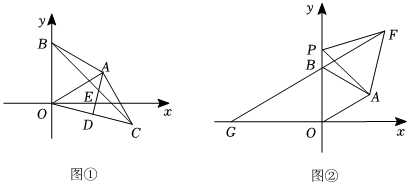
（1）請判斷△ABO的形狀，并說明理由；
（2）如圖①，AO⊥AC，且AO=AC，點D為OC的中點，BC和AD交于點E，求證：BE=AE+EC；
（3）如圖②，點P在點B的上方運動，以AP為邊在第一象限內作一個等邊△APF，延長FB交x軸于點G．問：
BG與AO之間有何數量關系，試證明你的結論．
【考點】三角形綜合題．
【答案】（1）△ABO是等邊三角形，理由見解答；
（2）證明見解答；
（3）BG=2OA，證明見解答．
（2）證明見解答；
（3）BG=2OA，證明見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 3:0:2組卷：301引用：1難度：0.3
相似題
-
1．角平分線性質定理描述了角平分線上的點到兩邊距離的關系，小明發現將角平分線放在三角形中，還可以得出一些線段比例的關系．
請完成下列探索過程：
【研究情景】
如圖1，在△ABC中，∠ABC的角平分線交AC于點D．
【初步思考】
（1）若AB=4，BC=7，則=；S△ABDS△CBD
【深入探究】
（2）請判斷和ABBC之間的數值關系，并證明；ADCD
【應用遷移】
（3）如圖2，△ABC和△ECD都是等邊三角形，△ABC的頂點A在△ECD的邊ED上，CD交AB于點F，若AE=4，AD=2，求△CFB的面積．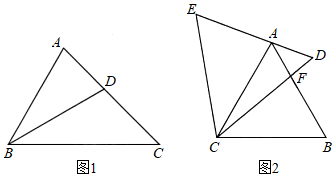
發布：2025/6/4 19:30:1組卷：722引用：3難度：0.4 -
2．如圖，三角形ABC中，AB⊥BC，AB=BC=4，E為線段AC上任意一點，P是BC的中點，連接PE，作PF垂直于PE且滿足PF=PE（點F與點B在直線EP同側），連接EF，直線EF交AB于點G．
（1）根據題意補全圖1；若，則EP的長為 ；AE=2
（2）若點G恰好是線段EF的中點，連接BF，證明：AC=4BF且AC⊥BF．
（3）作點B關于直線PF的對稱點Q．連接AQ，PQ，當AQ+PQ取最小值時，直接寫出此時△ABQ的面積．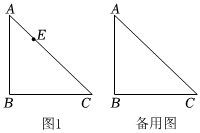
發布：2025/6/4 19:0:1組卷：107引用：1難度：0.3 -
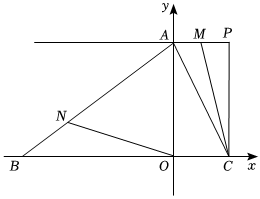3．如圖，C為x軸正半軸上一動點，A（0，a），B（b,0），且a,b滿足=0，AB=10．a-6+（b+8）2
（1）求△ABO的面積；
（2）求點O到AB的距離；
（3）如圖2，若P（3，6），PC⊥x軸于點C，點M從點P出發，在射線PA上運動，同時另一動點N從點B出發向點A運動，到點A時兩點停止運動，M，N的速度分別為2個單位長度/秒，3個單位長度/秒，當S△MAC=時，求點M的坐標．13S△BON發布：2025/6/4 19:0:1組卷：138引用：1難度：0.5