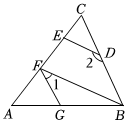
如圖，已知∠AGF=∠ABC，∠1+∠2=180°．
（1）試判斷BF與DE的位置關系，并說明理由；
（2）若DE⊥AC，∠2=140°，求∠AFG的度數．
?
【考點】平行線的判定與性質．
【答案】（1）見解答：（2）50°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：329引用：9難度：0.6
相似題
-
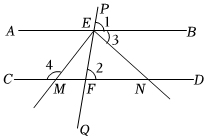1．完成證明并寫出推理根據：
如圖，直線PQ分別與直線AB、CD交于點E和點F，∠1=∠2，射線EM、EN分別與直線CD交于點M、N，且EM⊥EW，則∠4與∠3有何數量關系？并說明理由．
解：∠4與∠3的數量關系為 ，理由如下：
∵∠1=∠2（已知），
∴∥（ ），
∴∠4=∠（ ），
∵EM⊥EN（已知），
∴∠MEN=90°（ ），
∵∠BEM-∠3=∠，
∴∠4=∠3+．發布：2025/6/8 11:0:1組卷：30引用：1難度：0.5 -
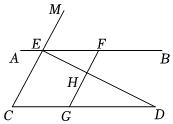2．如圖，已知點E、F在直線AB上，點G在線段CD上，ED與FG交于點H，∠C=∠EFG，∠CED=∠GHD．
（1）求證：CE∥GF；
（2）試判斷∠AED與∠D之間的數量關系，并說明理由；
（3）若∠D=30°，求∠AED的度數．發布：2025/6/8 11:30:1組卷：520引用：4難度：0.6 -
3．如圖1，已知AB∥CD，直線AB、CD把平面分成①、②、③三個區域（直線AB、CD不屬于①、②、③中任何一個區域）．點P是直線AB、CD、AC外一點，聯結PA、PC，可得∠PAB、∠PCD、∠APC．
（1）如圖2，當點P位于第①區域一位置時，請填寫∠APC=∠PAB+∠PCD的理由．
解：過點P作PE∥AB，
因為AB∥CD，PE∥AB，
所以PE∥CD（）．
因為PE∥AB，
所以∠APE=∠PAB（）．
同理∠CPE=∠PCD．
因此∠APE+∠CPE=∠PAB+∠PCD．
即∠APC=∠PAB+∠PCD．
（2）在第（1）小題中改變點P的位置，如圖3所示，求∠APC+∠PAB+∠PCD等于多少度？為什么？
（3）當點P在第②區域時，∠PAB、∠PCD、∠APC有怎樣的數量關系？請畫出圖形，并直接寫出相應的結論．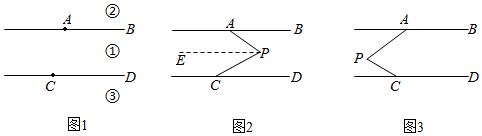
發布：2025/6/8 12:30:1組卷：107引用：3難度：0.6