定義：兩邊的平方和等于第三邊平方的兩倍的三角形叫做“漂亮三角形”．
（1）根據“漂亮三角形”的定義，判斷：
①命題“等邊三角形一定是漂亮三角形”是 真真命題
②命題“若等腰三角形是漂亮三角形，則它一定是等邊三角形”是 真真命題；（填“真”或“假”）
（2）在Rt△ABC中，∠ACB=90°，AB=c,AC=b,BC=a,且b＞a,若Rt△ABC是“漂亮三角形”，求a：b：c的值；
（3）如圖，在四邊形ACBD中，∠ACB=∠ADB=90°，AD=BD，若在四邊形ACBD內存在點E使得AE=AD，CB=CE．
①求證：△ACE是“漂亮三角形”；
②當△ACE是直角三角形時，且AC=3，求線段AB的長．
AC
=
3
【考點】四邊形綜合題．
【答案】真；真
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：66引用：3難度：0.1
相似題
-
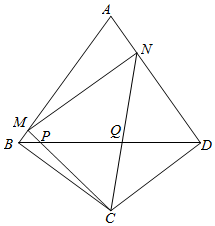1．如圖，四邊形ABCD中，AB=AD=4，CB=CD=3，∠ABC=∠ADC=90°，點M、N是邊AB、AD上的動點，且∠MCN=∠BCD，CM、CN與對角線BD分別交于點P、Q．12
（1）求sin∠MCN的值；
（2）當DN=DC時，求∠CNM的度數；
（3）試問：在點M、N的運動過程中，線段的比值是否發生變化？如不變，請求出這個值；如變化，請至少給出兩個可能的值，并說明點N相應的位置．PQMN發布：2025/6/10 13:0:2組卷：1113引用：6難度：0.1 -
2．在Rt△ABC和Rt△CDE中，AC=BC=a,CD=CE=b（b＜a），∠ACB=∠DCE=90°，如圖（1），以AC，CE為邊作平行四邊形ACEM，以CD，CB為邊作平行四邊形BCDN，點F，G分別是CM，BD的中點，當△DCE繞點C旋轉時，
（1）證明：△MCA≌△DBC；
（2）①求△CFG的面積（用含a,b的代數式表示）；
②直接寫出FG的長度的最大值為（用含a,b的代數式表示）．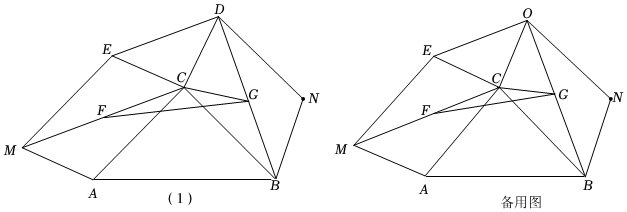
發布：2025/6/10 15:0:1組卷：107引用：2難度：0.1 -
3．如圖，矩形紙片ABCD中，AB=8，將紙片折疊，使頂點B落在邊AD上的E點處，折痕的一端G點在邊BC上．
（1）如圖1，當折痕的另一端F在邊AB上，且時，則∠BGE=；AF=83
（2）如圖2，當折痕的另一端F在邊AD上，點E與D點重合時，判斷△FHD和△DCG是否全等？請說明理由．
（3）若BG=10，當折痕的另一端F在邊AD上，點E未落在邊AD上，且點E到AD的距離為2時，直接寫出AF的長．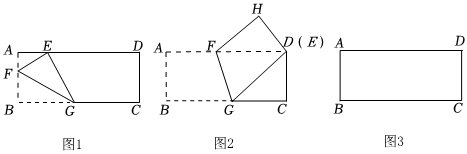
發布：2025/6/10 15:30:2組卷：546引用：6難度：0.3