已知正方形ABCD和等腰直角三角形AEF，∠EAF=90°，連接BD，BE，BF，DE，點G，H，I分別為線段BD，BF，DE的中點，連接GH，GI，HI．
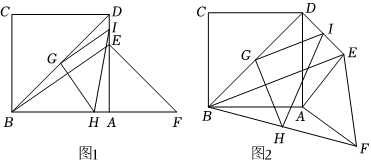
（1）如圖1，當點B，A，F在一條直線上時，請直接寫出線段GH與GI的關系；
（2）如圖2，將△AEF繞點A順時針旋轉α（0°＜α＜90°），判斷線段GH與GI的關系，并說明理由；
（3）在（2）的條件下，若AB=4，AE=3，△ADE，△ABF，△GHI的面積分別為S1，S2，S．
①請直接寫出S1與S2大小關系；
②直接寫出S-S1+S24的值．
S
-
S
1
+
S
2
4
【考點】四邊形綜合題．
【答案】（1）GH=GI且GH⊥GI；
（2）GH=GI且GH⊥GI，理由見解答過程；
（3）①S1=S2，
②．
（2）GH=GI且GH⊥GI，理由見解答過程；
（3）①S1=S2，
②
25
8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/21 16:0:1組卷：155引用：2難度：0.1
相似題
-
1．如圖1，四邊形ABCD是正方形，M是BC邊上的一點，E是CD邊的中點，
AE平分∠DAM．
（1）寫出AM、AD、MC三條線段的數量關系：；
請對你猜想的結論進行證明；
（2）寫出AM、DE、BM三條線段的數量關系：.（不必證明）
拓展延伸：
若四邊形ABCD是長與寬不相等的矩形，其他條件不變，如圖2，（1）、（2）中的結論是否成立？請分別作出判斷，不需要證明．
發布：2025/5/21 19:0:1組卷：44引用：4難度：0.3 -
2．【問題再現】：
（1）如圖1，平行四邊形ABCD的對角線交于點O，點E，F在對角線BD上，連接AE，CF．若再增加一個條件，便可證明出AE=CF．
針對上述問題，小明添加的條件是“DE=BF”；小強添加的條件是“AE∥CF”．請你替小明或小強完成證明過程；（即任選其中一種方法證明）
【問題探究】：
（2）如圖2，平行四邊形ABCD的對角線交于點O，過點B的直線與對角線AC交于點P，分別過點A，C作直線BP的垂線，垂足分別為點E，F，連接OE，OF．
①求證：OE=OF；
②若∠OEF=30°，探究AE，CF，OE間的等量關系，并證明；
【問題拓廣】：
（3）如圖3，平行四邊形ABCD的對角線交于點O，過點B的直線與對角線CA的延長線交于點P，分別過點A，C作直線BP的垂線，垂足分別為點E，F，連接OE，OF．若∠OEF的度數記為α，請寫出AE，CF，OE間的等量關系，并證明．
發布：2025/5/21 22:0:1組卷：168引用：3難度：0.1 -
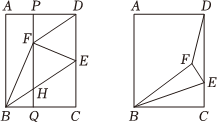3．在矩形ABCD中，點E為線段CD上一動點，將△BCE沿BE折疊得到△BFE，點C的對應點是F，連接DF．
（1）如圖1，BC＞AB，若點E為CD的中點時，過點F作PQ⊥BC于點Q，分別交AD，BE于點P，H．給出下列結論：12
①DF∥EH；
②HF=PF+HQ；
③△EFH為等邊三角形，請任意選擇一個你認為正確的結論加以證明：
（2）如圖2，若BC=3，AB=4．
①在點E運動過程中，當DF取得最小值時，求DE的長；
②設CE=x,tan∠ABF為y,求y關于x的函數關系．發布：2025/5/21 21:0:1組卷：463引用：1難度：0.4
相關試卷