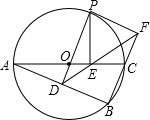
如圖，⊙O是△ABC的外接圓，AC是直徑，過點(diǎn)O作OD⊥AB于點(diǎn)D，延長DO交⊙O于點(diǎn)P，過點(diǎn)P作PE⊥AC于點(diǎn)E，作射線DE交BC的延長線于F點(diǎn)，連接PF．
（1）若∠POC=60°，AC=12，求劣弧PC的長；（結(jié)果保留π）
（2）求證：OD=OE；
（3）求證：PF是⊙O的切線．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/30 8:0:9組卷：8021引用：71難度：0.3
相似題
-
1．已知：如圖，⊙O與⊙P相交于A、B兩點(diǎn)，點(diǎn)P在⊙O上，⊙O的弦AC切⊙P于點(diǎn)A，CP及其延長線交⊙P于D、E，過點(diǎn)E作EF⊥CE交CB的延長線于F．
（1）求證：BC是⊙P的切線；
（2）若CD=2，CB=，求EF的長；22
（3）求以BP、EF為根的一元二次方程．發(fā)布：2025/5/29 3:30:1組卷：107引用：3難度：0.1 -
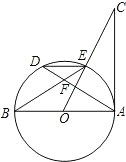2．已知：如圖，AB是⊙O的直徑，AD是弦，OC垂直AD于F交⊙O于E，連接DE、BE，且∠C=∠BED．
（1）求證：AC是⊙O的切線；
（2）若OA=10，AD=16，求AC的長．發(fā)布：2025/5/29 1:30:1組卷：772引用：42難度：0.1 -
3．如圖，以等腰△ABC的一腰AB為直徑的⊙O交BC于D，過D作DE⊥AC于E，可得結(jié)論：DE是⊙O的切線．問：
（1）若點(diǎn)O在AB上向點(diǎn)B移動(dòng)，以O(shè)為圓心，OB長為半徑的圓仍交BC于D，DE⊥AC的條件不變，那么上述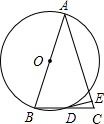
結(jié)論是否成立？請(qǐng)說明理由；
（2）如果AB=AC=5cm,sinA=，那么圓心O在AB的什么位置時(shí)，⊙O與AC相切？35發(fā)布：2025/5/29 5:30:2組卷：103引用：6難度：0.1