問題探究
(1)如圖①,點B,C分別在AM,AN上,AM=18米,AN=30米,AB=4.5米,BC=4.2米,AC=2.7米,求MN的長.
問題解決
(2)如圖②,四邊形ACBD規劃為園林綠化區,對角線AB將整個四邊形分成面積相等的兩部分,已知AB=60米,四邊形ACBD的面積為2400平方米,為了更好地美化環境,政府計劃在AC,BC邊上分別確定點E,F,在AB邊上確定點P,Q,使四邊形EFPQ為矩形,在矩形EFPQ內種植花卉,在四邊形ACBD剩余區域種植草坪,為了方便市民觀賞,計劃在FQ之間修一條小路,并使得FQ最短,根據設計要求,求出FQ的最小值,并求出當FQ最小時花卉種植區域的面積.
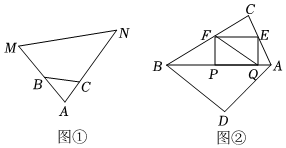
【考點】相似三角形的判定與性質;二次函數的性質.
【答案】(1)28米;
(2)FQ的最小值為米,此時花卉種植區域的面積為平方米.
(2)FQ的最小值為
120
13
13
86400
169
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:393引用:2難度:0.4
相似題
-
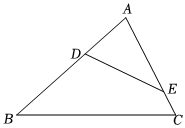 1.如圖,點D、E分別在△ABC邊AB、AC上,,且∠AED=∠B,那么ABAD=AECE=3的值為( )ADAC
1.如圖,點D、E分別在△ABC邊AB、AC上,,且∠AED=∠B,那么ABAD=AECE=3的值為( )ADACA. 12B. 13C. 14D. 23發布:2025/5/24 9:30:2組卷:474引用:3難度:0.5 -
 2.如圖,AB=10,點C是射線BQ上的動點,連結AC,作CD⊥AC,CD=AC,動點E在AB延長線上,tan∠QBE=3,連結CE,DE,當CE=DE,CE⊥DE時,BE的長是 .發布:2025/5/24 8:30:1組卷:2438引用:4難度:0.3
2.如圖,AB=10,點C是射線BQ上的動點,連結AC,作CD⊥AC,CD=AC,動點E在AB延長線上,tan∠QBE=3,連結CE,DE,當CE=DE,CE⊥DE時,BE的長是 .發布:2025/5/24 8:30:1組卷:2438引用:4難度:0.3 -
 3.如圖,平行四邊形ABCD中,點E在CD邊上,連接BE,∠ABE=60°,F在BE上,AF=CE,∠BAF=∠CBE,若AD=7,AB=6,則BF=.發布:2025/5/24 8:30:1組卷:302引用:2難度:0.5
3.如圖,平行四邊形ABCD中,點E在CD邊上,連接BE,∠ABE=60°,F在BE上,AF=CE,∠BAF=∠CBE,若AD=7,AB=6,則BF=.發布:2025/5/24 8:30:1組卷:302引用:2難度:0.5


