【概念認識】
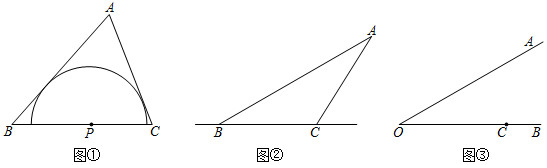
若以三角形某邊上任意一點為圓心，所作的半圓上的所有點都在該三角形的內部或邊上，則將符合條件且半徑最大的半圓稱為該邊關聯的極限內半圓．
如圖①，點P是銳角△ABC的邊BC上一點，以P為圓心的半圓上的所有點都在△ABC的內部或邊上．當半徑最大時，半圓P為邊BC關聯的極限內半圓．
【初步思考】
若等邊△ABC的邊長為1，則邊BC關聯的極限內半圓的半徑長為 3434．
如圖②，在鈍角△ABC中，用直尺和圓規作出邊BC關聯的極限內半圓（保留作圖痕跡，不寫作法）．
【深入研究】
如圖③，∠AOB=30°，點C在射線OB上，OC=6，點Q是射線OA上一動點．在△QOC中，若邊OC關聯的極限內半圓的半徑為r,當1≤r≤2時，求OQ的長的取值范圍．
3
4
3
4
【答案】
3
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/28 15:0:2組卷：1064引用：4難度：0.4
相似題
-
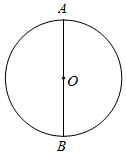1．下面是某同學設計的“作已知圓的內接正三角形”的尺規作圖過程．
已知：⊙O．
求作：⊙O的內接正三角形．
作法：如圖，
①作直徑AB；
②以B為圓心，OB為半徑作弧，與⊙O交于C，D兩點；
③連接AC，AD，CD．
所以△ACD就是所求的三角形．
根據該同學設計的尺規作圖過程．
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明：
證明：在⊙O中，連接OC，OD，BC，BD，
∵OC=OB=BC，
∴△OBC為等邊三角形（ ）（填推理的依據）．
∴∠BOC=60°．
∴∠AOC=180°-∠BOC=120°．
同理∠AOD=120°，
∴∠COD=∠AOC=∠AOD=．
∴AC=CD=AD（ ）（填推理的依據）．
∴△ACD是等邊三角形．發布：2025/5/26 6:0:1組卷：70引用：1難度：0.5 -
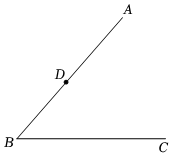2．如圖，已知△ABC，點D是BA邊上一點．
（1）在BC上截取BE=BD，連接DE．以點D為頂點，以DA為一邊，在∠ABC內作∠ADF=∠ABC；
（2）根據你的作圖，證明DE平分∠BDF．發布：2025/5/26 7:30:2組卷：46引用：1難度：0.5 -
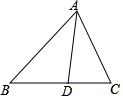3．如圖，AD是△ABC的角平分線，請利用尺規作圖法，在AB，AC邊上分別求作點E、點F，使四邊形AEDF是菱形．（保留作圖痕跡，不寫作法）發布：2025/5/26 5:0:1組卷：216引用：4難度：0.7