如圖，在圖1、圖2中，AB=6cm,點(diǎn)C在線(xiàn)段AB上，AC=2BC，直角三角板EOF（∠EOF=90°）的直角邊OE放在線(xiàn)段MN上，現(xiàn)將一動(dòng)點(diǎn)P沿A→B→A方向以1cm/秒的速度向右勻速運(yùn)動(dòng)，時(shí)間為t秒（0≤t≤12），同時(shí)將直角三角板EOF繞點(diǎn)O以30°/秒的速度順時(shí)針勻速旋轉(zhuǎn)一周．
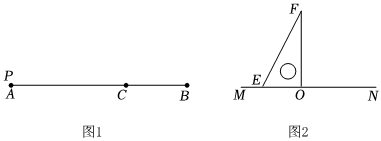
（1）BC=22cm；
（2）當(dāng)∠EOM=60°，求旋轉(zhuǎn)時(shí)間t的值；
（3）若∠EON=5∠FON，求此時(shí)線(xiàn)段PC的長(zhǎng)度．
【考點(diǎn)】三角形綜合題．
【答案】2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/29 14:0:2組卷：134引用：1難度：0.5
相似題
-
1．在平面直角坐標(biāo)系中，點(diǎn)A在x軸正半軸上，點(diǎn)B在y軸正半軸上，∠ABC=90°，且AB=BC．
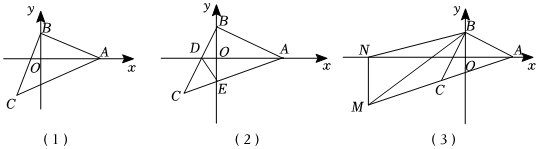
（1）如圖（1），A（5，0），B（0，2），點(diǎn)C在第三象限，請(qǐng)直接寫(xiě)出點(diǎn)C的坐標(biāo)；
（2）如圖（2），BC與x軸交于點(diǎn)D，AC與y軸交于點(diǎn)E，若點(diǎn)D為BC的中點(diǎn)，求證：∠ADB=∠CDE；
（3）如圖（3），A（a,0），M在A(yíng)C延長(zhǎng)線(xiàn)上，過(guò)點(diǎn)M（m,-a）作MN⊥x軸于N，探究線(xiàn)段BM，AN，OB之間的數(shù)量關(guān)系，并證明你的結(jié)論．發(fā)布：2025/5/31 4:30:2組卷：490引用：2難度：0.4 -
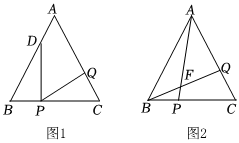2．如圖，在△ABC中，AB=AC=BC=4cm,如果點(diǎn)P在線(xiàn)段BC上以1cm/s的速度由B點(diǎn)向終點(diǎn)C運(yùn)動(dòng)，點(diǎn)Q在線(xiàn)段AC上以3的速度由A點(diǎn)向終點(diǎn)C運(yùn)動(dòng)，點(diǎn)D在線(xiàn)段BA上由B點(diǎn)向終點(diǎn)A運(yùn)動(dòng)（D點(diǎn)運(yùn)動(dòng)速度不能超過(guò)點(diǎn)Q）．三點(diǎn)同時(shí)運(yùn)動(dòng)，當(dāng)點(diǎn)Q停止運(yùn)動(dòng)，另兩點(diǎn)也隨之停止運(yùn)動(dòng)．
（1）如圖1，當(dāng)△BPD與△CQP全等時(shí)，D點(diǎn)的運(yùn)動(dòng)速度為多少？
（2）如圖2，當(dāng)BP=CQ時(shí)，連接點(diǎn)A與點(diǎn)P，連接點(diǎn)B與點(diǎn)Q，線(xiàn)段AP，BQ相交于點(diǎn)F，求∠AFQ的度數(shù)；
（3）若點(diǎn)Q改為在線(xiàn)段AC上沿A→C→A方向運(yùn)動(dòng)，其他條件不變，則點(diǎn)Q運(yùn)動(dòng) 秒時(shí)，PQ∥AB．發(fā)布：2025/5/31 4:30:2組卷：36引用：1難度：0.3 -
3．如圖①，在△ABC中，AB=AC，點(diǎn)P為邊BC上異于B和C的任意一點(diǎn)，過(guò)點(diǎn)P作PD⊥AB于D，作PE⊥AC于E，過(guò)點(diǎn)C作CF⊥AB于F，求證：PD+PE=CF．
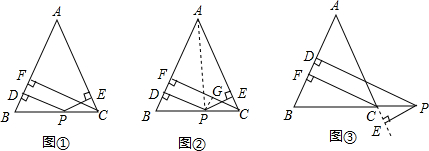
（1）有下面兩種證明思路：（一）如圖②，連接AP，由△ABP于△ACP面積之和等于△ABC的面積證得PD+PE=CF．（二）如圖②，過(guò)點(diǎn)P作PG⊥CF，垂足為G，可以證明：PD=GF，PE=CG，則PD+PE=CF．
請(qǐng)你選擇其中的一種證明思路完成證明：
（2）探究：如圖③，當(dāng)點(diǎn)P在BC的延長(zhǎng)線(xiàn)上時(shí)，其它條件不變，探究并證明PD、PE和CF間的數(shù)量關(guān)系；
（3）猜想：當(dāng)點(diǎn)P在CB的延長(zhǎng)線(xiàn)上時(shí)，其它條件不變，猜想PD、PE和CF間的數(shù)量關(guān)系（不要求證明）發(fā)布：2025/5/31 4:0:1組卷：315引用：2難度：0.1