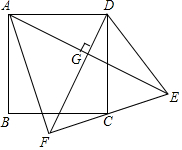
如圖，正方形ABCD中，AB=5，在邊CD的右側作等腰三角形DCE，使DC=DE，記∠CDE為α（0°＜α＜90°），連接AE，過點D作DG⊥AE，垂足為G，交EC的延長線于點F，連接AF．
（1）求∠DEA的大小（用α的代數式表示）；
（2）求證：△AEF為等腰直角三角形；
（3）當CF=2時，求點E到CD的距離．
5
2
【答案】（1）∠DEA=；
（2）證明過程見解答；
（3）點E到CD的距離為．
180
°
-
∠
ADE
2
=
45
°
-
α
2
（2）證明過程見解答；
（3）點E到CD的距離為
3
5
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：862引用：3難度：0.2
相似題
-
1．如圖，四邊形ABCD是正方形，△ABE是等腰三角形，AB=AE，∠BAE=θ（0°＜θ＜90°）．連接DE，過B作BF⊥DE于F，連接AF，CF．
（1）若θ=60°，求∠BED的度數；
（2）當θ變化時，∠BED的大小會發生變化嗎？請說明理由；
（3）試用等式表示線段DE與CF之間的數量關系，并證明．發布：2025/5/24 1:30:2組卷：1766引用：7難度：0.4 -
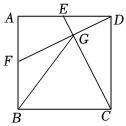2．如圖，在正方形ABCD中，點E，F分別是邊AD，AB的中點，連結CE，DF交于點G，連結BG．若EG=402，則BG=．發布：2025/5/24 0:30:1組卷：379引用：1難度：0.4 -
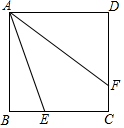3．已知正方形ABCD的邊長為2，E，F分別是邊BC，CD上的兩個動點，且滿足BE=CF，連接AE，AF，則AE+AF的最小值為 ．發布：2025/5/23 23:30:1組卷：1298引用：3難度：0.7