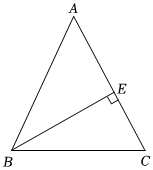
如圖，在△ABC中，AB=AC，BE⊥AC于E．
（1）用尺規作圖：過C點作CD⊥AB交AB于點D；（保留作圖痕跡，不寫作法和結論）
（2）在（1）的作法下，求證BD=CE．
證明：∵BE⊥AC，CD⊥AB，
∴①∠ADC=∠AEB=90°∠ADC=∠AEB=90°，
在△AEB和△ADC中，∠AEB=∠ADC=90° ∠A=∠A ②（??）
，
∴△AEB≌△ADC（AAS），
∴③AD=AEAD=AE，
∵AB=AC，
∴④AB-AD=AC-AEAB-AD=AC-AE，
∴BD=CE．
∠ AEB =∠ ADC = 90 ° |
∠ A =∠ A |
② （ ?? ） |
【考點】作圖—基本作圖；全等三角形的判定與性質．
【答案】∠ADC=∠AEB=90°；AD=AE；AB-AD=AC-AE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 10:0:1組卷：169引用：1難度：0.5
相似題
-
1．如圖，點C在∠AOB的OB邊上，用尺規作出了CN∥OA，作圖痕跡中，是（ ）?FG發布：2025/5/31 15:30:1組卷：1237引用：30難度：0.9 -
2．如圖，已知AC為⊙O的直徑，B為⊙O上一點．
（1）用尺規作圖：過點O作AB的垂線，垂足為D，交劣弧AB于點E；（只保留作圖痕跡）；
（2）根據（1）中作圖，若BC=6，AB=8，求DE的長，請回答下列解答過程中的序號①、②、③、④所對應的內容．
解：∵AC為⊙O的直徑，B為⊙O上一點，
∴∠ABC=；
在Rt△ABC中，BC=6，AB=8，
∴AC==10，AB2+BC2
∴OE=AC=5，12
∵OE為半徑，OE⊥AB，
∴AD=；
又∵CO=AO，
∴OD是△ABC的中位線，
∴=BC=3；12
∴DE=OE-OD=．發布：2025/5/31 15:0:2組卷：43引用：1難度：0.5 -
3．如圖，Rt△ABC中，∠A=90°．
（1）用尺規作圖法作∠ABD=∠C，與邊AC交于點D（保留作圖痕跡，不用寫作法）；
（2）在（1）的條件下，當∠C=30°時，求∠BDC的度數．發布：2025/5/31 15:0:2組卷：14引用：1難度：0.5