如圖，某日的錢塘江觀測(cè)信息如下：
2017年×月×日，天氣：陰；能見度：1.8千米；
11：40時(shí)，甲地“交叉潮”形成，潮水勻速奔向乙地；
12：10時(shí)，潮頭到達(dá)乙地，形成“一線潮”，開始均勻加速，繼續(xù)向西；
12：35時(shí)，潮頭到達(dá)丙地，遇到堤壩阻擋后回頭，形成“回頭潮”．
按上述信息，小紅將“交叉潮”形成后潮頭與乙地之間的距離s（千米）與時(shí)間t（分鐘）的函數(shù)關(guān)系用圖3表示．其中：“11：40時(shí)甲地‘交叉潮’的潮頭離乙地12千米”記為點(diǎn)A（0，12），點(diǎn)B坐標(biāo)為（m,0），曲線BC可用二次函數(shù)：s=1125t2+bt+c（b,c是常數(shù)）刻畫．
（1）求m值，并求出潮頭從甲地到乙地的速度；
（2）11：59時(shí)，小紅騎單車從乙地出發(fā)，沿江邊公路以0.48千米/分的速度往甲地方向去看潮，問她幾分鐘與潮頭相遇？
（3）相遇后，小紅立即調(diào)轉(zhuǎn)車頭，沿江邊公路按潮頭速度與潮頭并行，但潮頭過乙地后均勻加速，而單車最高速度為0.48千米/分，小紅逐漸落后．問小紅與潮頭相遇到落后潮頭1.8千米共需多長時(shí)間？（潮水加速階段速度v=v0+2125（t-30），v0是加速前的速度）
1
125
t
2
2
125
【考點(diǎn)】二次函數(shù)綜合題．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：78引用：2難度：0.3
相似題
-
1．如圖，拋物線y=ax2+bx+c經(jīng)過點(diǎn)A（-2，0），B（4，0），與y軸正半軸交于點(diǎn)C，且OC=2OA，拋物線的頂點(diǎn)為D，對(duì)稱軸交x軸于點(diǎn)E．直線y=mx+n經(jīng)過B，C兩點(diǎn)．
（1）求拋物線及直線BC的函數(shù)表達(dá)式；
（2）點(diǎn)F是拋物線對(duì)稱軸上一點(diǎn)，當(dāng)FA+FC的值最小時(shí)，求出點(diǎn)F的坐標(biāo)及FA+FC的最小值．
發(fā)布：2025/6/20 9:30:2組卷：197引用：4難度：0.5 -
2．如圖所示，在平面直角坐標(biāo)系xOy中，Rt△AOB的直角邊OB，OA分別在x軸上和y軸上，其中OA=2，OB=4，現(xiàn)將Rt△AOB繞著直角頂點(diǎn)O按逆時(shí)針方向旋轉(zhuǎn)90°得到△COD，已知一拋物線經(jīng)過C、D、B三點(diǎn)．
（1）該拋物線的解析式為；
（2）設(shè)點(diǎn)E是拋物線上位于第一象限的動(dòng)點(diǎn)，過點(diǎn)E作EF⊥x軸于點(diǎn)F，并交直線AB于N，過點(diǎn)E再作EM⊥AB于點(diǎn)M，求△EMN周長的最大值；
（3）當(dāng)△EMN的周長最大時(shí)，在直線EF上是否存在點(diǎn)Q，使得△QCD是以CD為直角邊的直角三角形？若存在請(qǐng)求出點(diǎn)Q的坐標(biāo)，若不存在，請(qǐng)說明理由．
發(fā)布：2025/6/20 10:0:1組卷：283引用：3難度：0.3 -
3．如圖，在平面直角坐標(biāo)系中，拋物線y=ax2-2ax+c與x軸交于A、B兩點(diǎn)，與y軸負(fù)半軸交于點(diǎn)C，且AB=4，OB=OC．
（1）求拋物線解析式；
（2）在直線x=2上是否存在點(diǎn)M，使∠BMA=2∠MAB？若存在，求M點(diǎn)坐標(biāo)；
（3）點(diǎn)P為y軸上C點(diǎn)下方一動(dòng)點(diǎn)，PM、PN分別與拋物線交于唯一公共點(diǎn)M、N，連接MN交y軸于Q，試探究PQ與CQ的數(shù)量關(guān)系，并說明理由．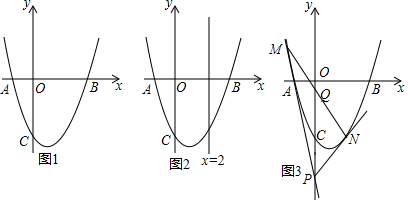
發(fā)布：2025/6/20 10:0:1組卷：244引用：2難度：0.2