綜合與實踐
問題情境：在“弘揚革命精神，傳承紅色基因”實踐活動中，同學們親自動手繪制了五角星，在制作過程中，每一個五角星的制作都會用到一個邊長為8cm的正方形．
動手操作：
步驟1：如圖1將正方形ABCD沿EF所在的直線對折，使BC與AD重合．
步驟2：將四邊形AEFD進行兩次折疊，使邊DF分別落在DA和EF邊上，折痕DG與FH相交于點O，展平后得圖2．
?步驟3：如圖3，將四邊形AEFD折疊，使點E與點O重合，折痕為MN．
?
步驟4：如圖4，將四邊形MNOA折疊，使NM與NO重合，隨后將∠FNO沿NO所在的直線折疊，即可得圖5．沿圖中虛線OP（使∠NOP＜30°）剪一刀，展開得圖6．
問題解決：
（1）圖1中，四邊形AEFD的形狀是 矩形矩形；圖6中∠POQ=36°，則圖5中∠NOP=18°18°．
（2）判斷圖2中，四邊形HDFG的形狀，并說明理由．
（3）請你直接寫出所做的五角星中，點O到中心點N的距離．
【考點】四邊形綜合題．
【答案】矩形；18°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/12 8:0:9組卷：218引用：1難度：0.2
相似題
-
1．（1）[方法回顧]：課本上“三角形中位線定理”的證明．已知：如圖1，在△ABC中，點D、E分別是邊AB、AC的中點．求證：DE=
BC，DE∥BC，證明：如圖1，延長DE到點F，使得EF=DE，連接CF；請繼續完成證明過程；12
（2）[問題解決]：如圖2，AB∥CD，E為AD的中點，G、F分別為射線AB、DC上的點，∠GEF=90°，線段AG、DF、FG有怎樣的數量關系？請說明理由；
（3）[思維拓展]：如圖3，在四邊形ABCD中，AD∥BC，∠A=∠GEF=90°，∠D=120°，E為AD的中點，G、F分別為AB、CD邊上的點，H是GF的中點，若AG=2，DF=6（注：23=3），EH的長為 ．12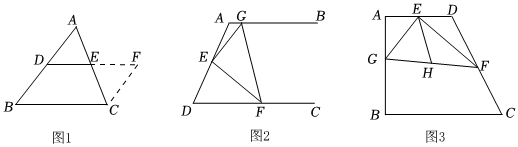
發布：2025/6/4 19:30:1組卷：242引用：2難度：0.1 -
2．如圖1，在四邊形ABCD中，E，F，G，H是各邊中點，連接EF，EH，HG，GF．可得到以下結論：
結論1：四邊形EFGH是平行四邊形；
結論2：四邊形EFGH的面積是四邊形ABCD的一半；
（1）試證明結論1．
（2）探究與應用：（提示：以下問題可以直接使用上述結論）
①如圖2，在四邊形ABCD中，E，G分別為邊AB，DC的中點，連接EG．已知AD=8，BC=6，求出線段EG的取值范圍．
②如圖3，在四邊形ABCD中，點E，F，G，H分別是AB，BC，CD，AD的中點，連接EG，FH交于點O，若HF=10，EG=7，∠EOH=60°，試求出四邊形ABCD的面積．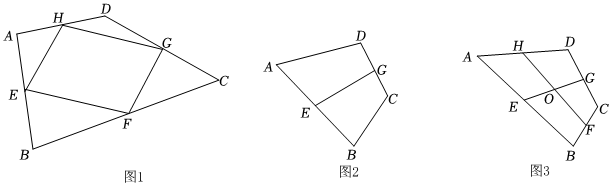
發布：2025/6/4 19:30:1組卷：95引用：1難度：0.1 -
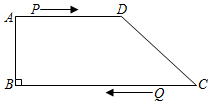3．如圖，在四邊形ABCD中，AD∥BC，∠B=90°，AB=8cm,AD=12cm,BC=18cm,點P從點A出發，以1cm/s的速度向點D運動；點Q從點C同時出發，以2cm/s的速度向點B運動．規定其中一個動點到達端點時，另一個動點也隨之停止運動．設點P，Q運動的時間為t s.
（1）CD邊的長度為 cm,t的取值范圍為 ．
（2）從運動開始，當t取何值時，PQ∥CD？
（3）從運動開始，當t取何值時，PQ=CD？
（4）在整個運動過程中是否存在t值，使得四邊形PQCD是菱形？若存在，請求出t值；若不存在，請說明理由．發布：2025/6/4 18:30:2組卷：259引用：3難度：0.2