問題發現：
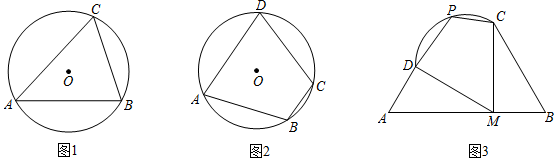
（1）如圖1，△ABC內接于半徑為4的⊙O，若∠C=60°，則AB=4343；
問題探究：
（2）如圖2，四邊形ABCD內接于半徑為6的⊙O，若∠B=120°，求四邊形ABCD的面積最大值；
解決問題：
（3）如圖3，一塊空地由三條直路（線段AD、AB、BC）和一條弧形道路?CD圍成，點M是AB道路上的一個地鐵站口，已知AD=BM=1千米，AM=BC=2千米，∠A=∠B=60°，?CD的半徑為1千米，市政府準備將這塊空地規劃為一個公園，主入口在點M處，另外三個入口分別在點C、D、P處，其中點P在?CD上，并在公園中修四條慢跑道，即圖中的線段DM、MC、CP、PD，是否存在一種規劃方案，使得四條慢跑道總長度（即四邊形DMCP的周長）最大？若存在，求其最大值；若不存在，說明理由．
3
3
?
CD
?
CD
?
CD
【考點】圓的綜合題．
【答案】4
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：927引用：5難度：0.3
相似題
-
1．如圖，平面直角坐標系中，已知點A（-1，0），B（-1，1），C（1，0），D（1，1），記線段AB為T1，線段CD為T2，點P是坐標系內一點．給出如下定義：若存在過點P的直線l與T1，T2都有公共點，則稱點P是T1-T2聯絡點．
例如，點P（0，）是T1-T2聯絡點．12
（1）點E（0，2），H（-4，2），K（3，2）中，是T1-T2聯絡點的是 ．（填出所有正確的點的坐標）；
（2）直接在圖1中畫出所有T1-T2聯絡點所組成的區域，用陰影部分表示；
（3）已知點M在y軸上，以M為圓心，x為半徑畫圓，⊙M上只有一個點為T1-T2聯絡點，求x的取值范圍．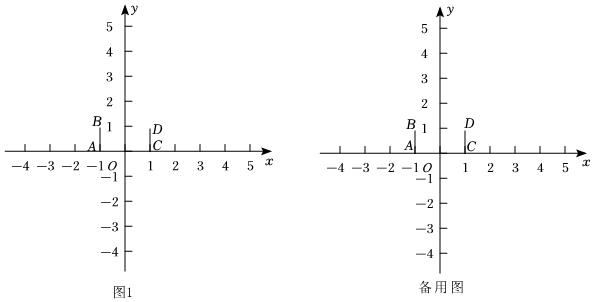
發布：2025/5/26 1:0:1組卷：92引用：1難度：0.3 -
2．如圖，Rt△ABC中，AB=AC，∠BAC=90°，BC=6cm,點M，N是邊BC上的兩個動點，點M從點B出發沿著BC以每秒1cm的速度向終點C運動；點N同時從點C出發沿著CB以每秒2cm的速度向終點B運動．設運動時間為t秒．
（1）當t=1時，求△AMN的面積．
（2）當t為何值時，∠MAN=45°．
（3）當以MN為直徑的圓與△AMN的邊有且只有三個公共點時，請直接寫出t的取值范圍．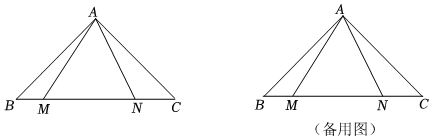
發布：2025/5/26 0:0:1組卷：335引用：2難度：0.3 -
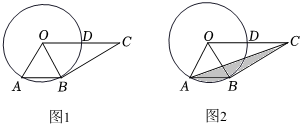3．如圖，點C為⊙O外一點，BC切⊙O于點B，弦AB∥OC，OC交⊙O于D．
（1）如圖1，連接BD，當∠AOB=度時，四邊形OABD是菱形；
（2）在（1）的條件下，
①試探究AB與BC的數量關系，并說明理由；
②如圖2，連接AC，若⊙O的半徑為2，陰影部分的面積為 （結果保留π）．發布：2025/5/25 21:30:1組卷：54引用：1難度：0.4