某企業電腦配件從去年1至9月原材料價格一路攀升，每件配件的原材料價格y1（元）與月份x（1≤x≤9，且x取整數）之間的函數關系如下表：
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 價格y1（元/件） | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
（1）直接寫出y1與x之間的函數關系式以及y2與x之間滿足的一次函數關系式；
（2）若去年該配件每件的售價為1000元，生產每件配件的人力成本為50元，其它成本30元，該配件在1至9月的銷售量p1（萬件）與月份x滿足關系式p1=0.1x+1.1（1≤x≤9，且x取整數），10至12月的銷售量p2（萬件）p2=-0.1x+2.9（10≤x≤12，且x取整數）．求去年哪個月銷售該配件的利潤最大，并求出這個最大利潤．
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：333引用：3難度：0.5
相似題
-
1．2022年12月7日我國疫情防控全面放開，某藥店為滿足居民的購藥需求，購進了一種中草藥，每千克成本為50元．市場調查發現，在一段時間內，銷售量w（千克）隨銷售單價x（元/千克）的變化而變化，具體關系式為：w=-2x+240，且物價部門規定這種中草藥的銷售單價不得高于90元/千克．設這種中草藥在這段時間內的銷售利潤為y（元）：
（1）求y與x的關系式；并求x取何值時，y的值最大？
（2）如果該藥店想要在這段時間內獲得2250元的銷售利潤，銷售單價應定為每千克多少元？發布：2025/5/30 12:0:2組卷：242引用：5難度：0.6 -
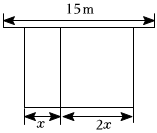2．【材料閱讀】
先閱讀理解下面的例題，再按要求解答下列問題：
我們知道a2≥0，所以代數式a2的最小值為0，可以用公式a2±2ab+b2=（a±b）2來求一些多項式的最小值．
例題：求代數式y2+4y+8的最小值．
解：y2+4y+8=y2+4y+4+4=（y+2）2+4．
∵（y+2）2≥0
∴（y+2）2+4≥4
∴代數式y2+4y+8的最小值為4．
請應用上述思想方法，解決下列問題：
【類比探究】（x-2）2+2的最小值為 ；
【舉一反三】
代數式-x2+8x有最 （填“大”或“小”）值為 ；
【靈活運用】
某農場計劃建造一個矩形養殖場，為充分利用現有資源，該矩形養殖場一面靠墻（墻的長度為15m），另外三面用柵欄圍成，中間再用柵欄把它分成兩個面積為1：2的矩形．已知柵欄的總長度為24m,則可設較小矩形的寬為x m,較大矩形的寬為2x m（如圖）．當x為多少時，矩形養殖場的總面積最大？最大值為多少？發布：2025/5/30 11:30:2組卷：202引用：2難度：0.6 -
3．小李在景區銷售一種旅游紀念品，已知每件進價為6元，當銷售單價定為8元時，每天可以銷售200件，市場調查反映：銷售單價每提高1元，日銷量將會減少10件，物價部門規定，銷售單價不能超過12元，設該紀念品的銷售單價為x（元），日銷量為y（件），日銷售利潤為w（元）．
（1）求y與x的函數關系式；
（2）要使日銷售利潤為720元，銷售單價應定為多少元？
（3）求日銷售利潤w（元）與銷售單價x（元）的函數關系式，當x為何值時，日銷售y所獲利潤最大．發布：2025/5/30 11:30:2組卷：142引用：1難度：0.4