【材料閱讀】
先閱讀理解下面的例題，再按要求解答下列問題：
我們知道a2≥0，所以代數式a2的最小值為0，可以用公式a2±2ab+b2=（a±b）2來求一些多項式的最小值．
例題：求代數式y2+4y+8的最小值．
解：y2+4y+8=y2+4y+4+4=（y+2）2+4．
∵（y+2）2≥0
∴（y+2）2+4≥4
∴代數式y2+4y+8的最小值為4．
請應用上述思想方法，解決下列問題：
【類比探究】（x-2）2+2的最小值為 22；
【舉一反三】
代數式-x2+8x有最 大大（填“大”或“小”）值為 1616；
【靈活運用】
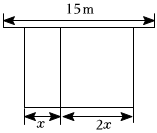
某農場計劃建造一個矩形養殖場，為充分利用現有資源，該矩形養殖場一面靠墻（墻的長度為15m），另外三面用柵欄圍成，中間再用柵欄把它分成兩個面積為1：2的矩形．已知柵欄的總長度為24m,則可設較小矩形的寬為x m,較大矩形的寬為2x m（如圖）．當x為多少時，矩形養殖場的總面積最大？最大值為多少？
【考點】二次函數的應用．
【答案】2；大；16
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 11:30:2組卷：202引用：2難度：0.6
相似題
-
1．下面的三個問題中都有兩個變量：
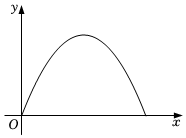
①將一根長為1的鐵絲剛好圍成一個矩形，矩形的面積y與矩形一條邊長x；
②趙老師爬香山所花的時間y和平均速度x；
③中秋節后，某超市月餅賣不出去，決定促銷，月餅原價為30元/kg,成本價為10元/kg,單價每降價1元，可以多賣出10kg,月餅利潤y與降價x；
其中，變量y與變量x之間的函數關系可以用如圖所示的圖象表示的是（ ）發布：2025/5/31 15:30:1組卷：212引用：6難度：0.6 -
2．某商場銷售一批名牌襯衫，平均每天可售出20件，每件盈利40元，為了擴大銷售，增加盈利，盡快減少庫存，商場決定采取適當降價措施，經調查發現，如果每件襯衫每降價一元，商場平均每天可多售出2件．
①若商場平均每天盈利1200元，每件襯衫應降價多少元？
②每件襯衫降價多少元時，商場平均每天利潤最大，最大利潤是多少元？發布：2025/5/31 15:30:1組卷：386引用：5難度：0.7 -
3．某公司對一種新型產品的產銷情況進行了營銷調查，發現年產量為x（噸）時，所需的費用y（萬元）與（x2+60x+800）成正比例，投入市場后當年能全部售出，且發現每噸的售價p（單位：萬元）由基礎價與浮動價兩部分組成，其中基礎價是固定不變的，浮動價與x成正比例，比例系數為-
．在營銷中發現年產量為20噸時，所需的全部費用是240萬元，并且年銷售利潤W最大值為55萬元．（注：年利潤=年銷售額-全部費用）120
（1）求y（萬元）與x（噸）之間滿足的函數關系式；
（2）求年銷售利潤W與年產量x（噸）之間滿足的函數關系式；
（3）當年銷售利潤最大時，每噸的售價是多少萬元？發布：2025/5/31 16:0:2組卷：186引用：3難度：0.5