應用題：深圳某學校為構建書香校園，擬購進甲、乙兩種規格的書柜放置新購置的圖書．已知每個甲種書柜的進價比每個乙種書柜的進價高10%，用3300元購進的甲種書柜的數量比用4500元購進的乙種書柜的數量少5臺．
（1）求甲、乙兩種書柜的進價；
（2）若該校擬購進這兩種規格的書柜共60個，其中乙種書柜的數量不大于甲種書柜數量的2倍．請您幫該校設計一種購買方案，使得花費最少，并求出最少花費多少錢．
【答案】（1）每個甲種書柜的進價為330元，每個乙種書柜的進價為300元；
（2）購進甲種書柜20個，購進乙種書柜40個時花費最少，費用為18600元．
（2）購進甲種書柜20個，購進乙種書柜40個時花費最少，費用為18600元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 14:0:1組卷：1050引用：7難度：0.5
相似題
-
1．如圖1，已知直線l1：y=x+3，點B（0，b）在直線l1上，y=mx+n是過定點P（1，0）的一簇直線．嘉淇用繪圖軟件觀察m與n的關系，記y=mx+n過點B時的直線為l2．
（1）求b的值及l2的解析式；
（2）探究m與n的數量關系：當y=mx+n與y軸的交點為（0，1）時，記此時的直線為l3，l3與l1的交點記為A，求AB的長；
（3）當y=mx+n與直線l1的交點為整點（橫、縱坐標均為整數），且m的值也為整數時，稱y=mx+n為“美好直線”．
①在如圖2所示的視窗下（-2.5≤x≤2.5，-2.5≤y≤2.5），求y=mx+n為“美好直線”時m的值；
②視窗的大小不變，改變其可視范圍，且變化前后原點O始終在視窗中心．現將圖2中坐標系的單位長度變為原來的，使得在視窗內能看到所有“美好直線”與直線y=x+3的交點，求k的最小整數值．1k
發布：2025/5/22 14:30:2組卷：173引用：4難度：0.4 -
2．周末，父子二人在一段筆直的跑道上練習競走，兩人分別從跑道兩端開始勻速往返練習．在同一平面直角坐標系中，父子二人離同一端的距離s（米）與時間t（秒）的函數圖象如圖所示．
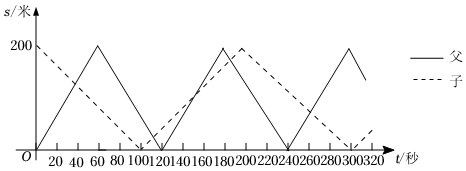
（1）父親的速度為 米/秒，兒子的速度為 米/秒；
（2）當200≤t≤300時，求兒子在競走過程中y與x之間的函數關系式；
（3）若不計轉向時間，按照這一速度練習10分鐘，父子迎面相遇的次數為 ．發布：2025/5/22 16:0:1組卷：161引用：2難度：0.4 -
3．為拓寬學生視野，我市某中學決定組織部分師生去廬山西海開展研學旅行活動，在參加此次活動的師生中，若每位老師帶17個學生，還剩12個學生沒人帶；若每位老師帶18個學生，就有一位老師少帶4個學生．為了安全，既要保證所有師生都有車坐，又要保證每輛客車上至少要有2名老師．現有甲、乙兩種大客車，它們的載客量和租金如表所示．
（1）參加此次研學旅行活動的老師和學生各有多少人？租用客車總數為多少輛？甲種客車 乙種客車 載客量/（人/輛） 30 42 租金/（元/輛） 300 400
（2）設租用x輛乙種客車，租車總費用為w元，請寫出w與x之間的函數關系式；
（3）在（2）的條件下，學校計劃此次研學旅行活動的租車總費用不超過3100元，租用乙種客車不少5輛，你能得出哪幾種不同的租車方案？其中哪種租車方案最省錢？請說明理由．發布：2025/5/22 16:0:1組卷：407引用：2難度：0.7