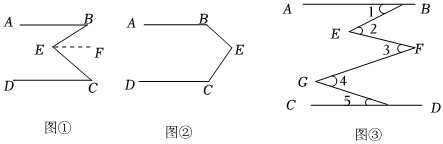
（1）問題發現：如圖①，直線AB∥CD，連接BE，CE，可以發現∠B+∠C=∠BEC．
請把下面的證明過程補充完整：
證明：過點E作EF∥AB，
∵AB∥DC（已知），EF∥AB（輔助線的作法），
∴EF∥DC（

平行于同一直線的兩直線平行

平行于同一直線的兩直線平行

）．
∴∠C=∠CEF．（

兩直線平行，內錯角相等

兩直線平行，內錯角相等

）．
∵EF∥AB，
∴∠B=∠BEF（同理）．
∴∠B+∠C=

∠BEF+∠CEF

∠BEF+∠CEF

．
即∠B+∠C=∠BEC．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，說明：∠B+∠BEC+∠C=360°．
（3）解決問題：如圖③，AB∥DC，E、F、G是AB與CD之間的點，直接寫出∠1，∠2，∠3，∠4，∠5之間的數量關系

∠1+∠3+∠5=∠2+∠4

∠1+∠3+∠5=∠2+∠4

．