數學活動課上，老師組織數學小組的同學們以“正方形折疊”為主題開展數學活動．
【動手實踐】
（1）如圖（1），已知正方形紙片ABCD，數學小組將正方形紙片沿過點A的直線折疊，使點B落在正方形ABCD的內部，點B的對應點為點M，折痕為AE，再將紙片沿過點A的直線折疊使AD與AM重合，折痕為AF，易知點E、M、F共線，則∠EAF=4545°，EF、BE、DF三條線段的關系為 EF=BE+DFEF=BE+DF；
【拓展應用】
（2）解決下面問題：
①如圖（2）作FN⊥AE于N，交AM于P，求證：△ANP≌△FNE；
②如圖（3），數學小組在圖（1）的基礎上進行如下操作：將正方形紙片沿EF繼續折疊，點C的對應點為點N，他們發現，當點E的位置不同時，點N的位置也不同，若點N恰好落在△AEF邊上，AB=3，請直接寫出此時BE的長度．
【考點】四邊形綜合題．
【答案】45；EF=BE+DF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/17 8:0:8組卷：362引用：4難度：0.3
相似題
-
1．【基礎鞏固】
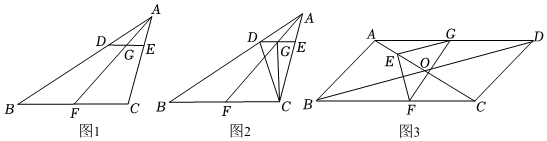
（1）如圖1，在△ABC中，D，E，F分別為AB，AC，BC上的點，DE∥BC，BF=CF，AF交DE于點G，求證：DG=EG．
【嘗試應用】
（2）如圖2，在（1）的條件下，連結CD，CG．若CG⊥DE，CD=10，AE=6，求的值．DEBC
【拓展提高】
（3）如圖3，在?ABCD中，∠ADC=45°，AC與BD交于點O，E為AO上一點，EG∥BD交AD于點G，EF⊥EG交BC于點F．若∠EGF=40°，FG平分∠EFC，FG=8，求BF的長．發布：2025/5/25 5:0:4組卷：1609引用：1難度：0.1 -
2．問題提出：
（1）如圖1，在矩形ABCD中，AB=4，AD=3，P是對角線AC上的一點，連接PD，將PD繞點P逆時針旋轉90°得到PM，過點M作MN⊥AC于N，求PN的長．
問題解決：
（2）2022年3月我省局部發生疫情，為落實“科學防治、精準施策、分級管理”，我省某小區設計防疫區域，在道路CD邊固定柱子（點Q），道路AB邊確定一點P，以PQ為邊，搭建正方形防疫區域PMNQ，內部道路CD上設點E作為記錄處，△EPQ、△EPM、△EMN、△ENQ分別為不同的防疫物資放置區域，設計圖簡化如圖2所示，已知道路兩邊AB∥CD，道路寬為6m,Q為CD上一定點，P為AB上一動點，PE⊥CD于E．請問是否存在符合設計要求且面積最小的△EMN？若存在，請求出面積最小值及此時QE的長；若不存在，請說明理由．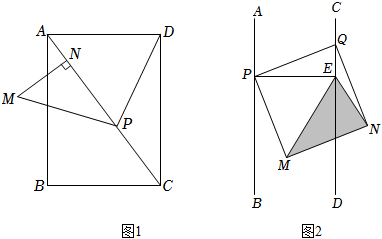
發布：2025/5/25 5:0:4組卷：214引用：2難度：0.1 -
3．【概念理解】定義：我們把對角線互相垂直的四邊形叫做垂美四邊形如圖①．
我們學習過的四邊形中是垂美四邊形的是 ；（寫出一種即可）
【性質探究】
利用圖①，垂美四邊形ABCD兩組對邊AB，CD的平方和與BC，AD的平方和之間的數量關系是 ；
【性質應用】
（1）如圖②，在△ABC中，BC=6，AC=8，D，E分別是AB，BC的中點，連接AE，CD，若AE⊥CD，則AB的長為 ；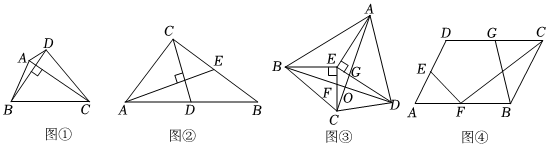
（2）如圖③，等腰Rt△BCE和等腰Rt△ADE中，∠BEC=∠AED=90°，AC與BD交于O點，BD與CE交于點F，AC與DE交于點G．若BE=6，AE=8，AB=12，求CD的長；
【拓展應用】如圖④，在?ABCD中，點E、F、G分別是AD、AB、CD的中點，EF⊥CF，AD=6，AB=8，求BG的長．發布：2025/5/25 5:0:4組卷：292引用：1難度：0.1