問題提出:
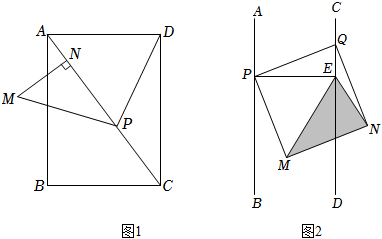
(1)如圖1,在矩形ABCD中,AB=4,AD=3,P是對角線AC上的一點,連接PD,將PD繞點P逆時針旋轉90°得到PM,過點M作MN⊥AC于N,求PN的長.
問題解決:
(2)2022年3月我省局部發生疫情,為落實“科學防治、精準施策、分級管理”,我省某小區設計防疫區域,在道路CD邊固定柱子(點Q),道路AB邊確定一點P,以PQ為邊,搭建正方形防疫區域PMNQ,內部道路CD上設點E作為記錄處,△EPQ、△EPM、△EMN、△ENQ分別為不同的防疫物資放置區域,設計圖簡化如圖2所示,已知道路兩邊AB∥CD,道路寬為6m,Q為CD上一定點,P為AB上一動點,PE⊥CD于E.請問是否存在符合設計要求且面積最小的△EMN?若存在,請求出面積最小值及此時QE的長;若不存在,請說明理由.
【考點】四邊形綜合題.
【答案】(1)PN的長為.
(2)△EMN的面積的最小值為,此時QE=3.
12
5
(2)△EMN的面積的最小值為
27
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/25 5:0:4組卷:214引用:2難度:0.1
相似題
-
1.如圖1,四邊形ABCD為正方形,點E為其邊BC上一點,以CE為邊在正方形ABCD右側作正方形CEFG,將正方形CEFG繞點C逆時針旋轉,記旋轉角為α(0°<α<360°),連接AF、BG,直線AF、BG交于點M.
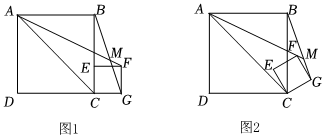
(1)當α=90°時,∠AMB=°;當α=270°時,∠AMB=°;
(2)在旋轉過程中,∠AMB的度數是否為定值?如果是,請就圖2的情況予以證明;如果不是,請說明理由.
(3)若BC=3,CE=1,當A、E、F三點在同一條直線上時,請直接寫出線段BM的長度.發布:2025/5/25 13:0:1組卷:152引用:1難度:0.1 -
2.在平行四邊形ABCD中,∠BCD=α,AD>AB,DE平分∠ADC交線段BC于點E,在?ABCD的外部作△BEF,使BF=EF,∠EBF=
α,連接AC,AF,線段AF與BC交于點N.12
(1)當α=120°時,請直接寫出線段AF和AC的數量關系;
(2)當α=90°時,
①請寫出線段AF,AB,AD之間的數量關系,并說明理由;
②若點E是BC的三等分點,請直接寫出sin∠BAN的值.發布:2025/5/25 11:30:2組卷:140引用:1難度:0.3 -
3.某數學興趣小組在數學課外活動中,對多邊形內兩條互相垂直的線段做了如下探究:

【觀察與猜想】
(1)如圖1,在正方形ABCD中,點E,F分別是AB,AD上的兩點,連接DE,CF,DE⊥CF,則的值為 ;DECF
【類比探究】
(2)如圖2,在矩形ABCD中,AD=7,CD=4,點E是AD上的一點,連接CE,BD,且CE⊥BD,求的值;CEBD
【拓展延伸】
(3)如圖,在四邊形ABCD中,∠A=∠B=90°,點E為AB上一點,連接DE,過點C作DE的垂線交ED的延長線于點G,交AD的延長線于點F,且AD=2,DE=3,CF=4.求AB的長.發布:2025/5/25 12:0:2組卷:620引用:6難度:0.2


