如圖1，已知兩條直線AB，CD被直線EF所截，分別交于點E，點F，EM平分∠AEF交CD于點M，且∠FEM=∠FME．
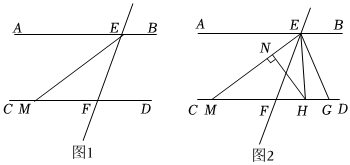
（1）判斷直線AB與直線CD是否平行，并說明理由；
（2）如圖2，點G是射線MD上一動點（不與點M，F重合），EH平分∠FEG交CD于點H，過點H作HN⊥EM于點N，設∠EHN=α，∠EGF=β．
①當點G在點F的右側時，若α=30°，直接寫出β的度數為 60°60°；
②當點G在運動過程中，直接寫出α和β之間的數量關系 α=12β或α=90°-12βα=12β或α=90°-12β．
α
=
1
2
β
α
=
90
°
-
1
2
β
α
=
1
2
β
α
=
90
°
-
1
2
β
【考點】平行線的判定與性質．
【答案】60°；或
α
=
1
2
β
α
=
90
°
-
1
2
β
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/6 8:0:9組卷：421引用：3難度：0.5
相似題
-
1．補全下面的解答過程．
如圖，AB∥CD，點E，F在直線CD下方，連接BE，DE，BF，DF．BF與CD交于點G．已知BE平分∠ABF，DE平分∠CDF，∠F=∠BGD，探究∠E與∠CDF的數量關系．12
解：∵AB∥CD，
∴∠ABF=∠（ ），
∵BE平分∠ABF
∴∠EBF=∠ABF，（ ），12
∵∠F=∠BGD，12
∴∠EBF=∠（ ），
∴BE∥DF（ ），
∴∠=∠EDF（ ），
∵DE平分∠CDF，
∴∠CDF=2∠EDF（
∴．發布：2025/6/7 9:30:1組卷：318引用：4難度：0.7 -
2．下列說法中，正確的有（ ）個．
①兩直線被第三條直線所截，同旁內角互補；
②同位角相等，兩直線平行；
③相等的角是對頂角；
④平行于同一條直線的兩條直線平行．發布：2025/6/7 9:30:1組卷：260引用：4難度：0.7 -
3．如圖1，直線MN與直線AB、CD分別交于點E、F，∠1與∠2互補．
（1）試判斷直線AB與直線CD的位置關系，并說明理由；
（2）如圖2，∠BEF與∠EFD的角平分線交于點P，EP與CD交于點G，點H是MN上一點，且GH⊥EG，求證：PF∥GH；
（3）如圖3，在（2）的條件下，連接PH，K是GH上一點使∠PHK=∠HPK，作PQ平分∠EPK，問∠HPQ的大小是否發生變化？請判斷結論，直接寫出答案，不用說明理由．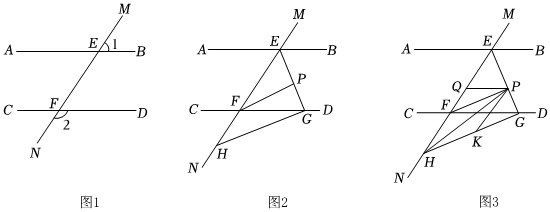
發布：2025/6/7 9:30:1組卷：264引用：3難度：0.5