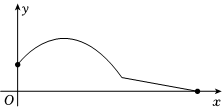
紙飛機是同學們很喜歡的娛樂項目．紙飛機的飛行一般會經歷上拋、下降、滑行三個階段，其中紙飛機上拋和下降的飛行路徑可看作是一段拋物線，滑行的飛行路徑是一條線段，滑行距離受紙飛機滑行比的影響（若紙飛機在1米的高度開始滑行，滑行的水平距離為n米，則滑行比為1：n）．如圖所示，若小明玩紙飛機，其起拋點的高度為1.9m,當紙飛機的最大高度達到2.8m時，它的水平飛行距離為3m.
（1）求這條拋物線的解析式；
（2）小明的前方有一堵2.5m高的墻壁，小明至少距離墻壁多遠，紙飛機才會順利飛過墻壁？（不考慮墻壁的厚度）
（3）小明根據多次實驗得到其折疊的紙飛機的滑行比為1：2.5（受空氣阻力的影響，紙飛機開始滑行的高度不超過1.4m），紙飛機開始滑行時的高度為多少米時，才能使水平飛行距離至少為10米？
【考點】二次函數綜合題．
【答案】（1）y=-0.1（x-3）2+2.8；（2）小明至少距離墻壁3-m時紙飛機才會順利飛過墻壁；（3）紙飛機開始滑行時的高度為1.2米時，才能使水平飛行距離至少為10米．
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/23 12:26:7組卷：496引用：3難度：0.4
相似題
-
1．如圖，拋物線與x軸交于A（x1，0），B（x2，0）兩點，且x1＜x2，與y軸交于點C（0，-5），其中x1，x2是方程x2-4x-5=0的兩個根．
（1）求這條拋物線的解析式；
（2）點M是線段AB上的一個動點，過點M作MN∥BC，交AC于點N，連接CM，當△CMN的面積最大時，求點M的坐標；
（3）點D（4，k）在（1）中拋物線上，點E為拋物線上一動點，在x軸是否存在點F，使以A，D，E，F四點為頂點的四邊形是平行四邊形？如果存在，直接寫出所有滿足條件的點F的坐標；如果不存在，請說明理由．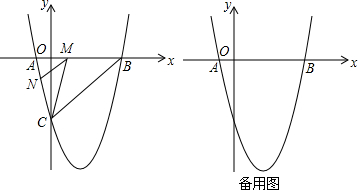
發布：2025/5/23 16:0:1組卷：388引用：4難度：0.3 -
2．如圖，拋物線y=ax2-2x+c與x軸相交于A（-1，0），B（3，0）兩點．
（1）求拋物線的函數表達式；
（2）點C在拋物線的對稱軸上，且位于x軸的上方，將△ABC沿直線AC翻折得到△AB'C，點B'恰好落在拋物線的對稱軸上．若點G為直線AC下方拋物線上的一點，求當△AB'G面積最大時點G的橫坐標；
（3）點P是拋物線上位于對稱軸右側的一點，在拋物線的對稱軸上存在一點Q使得△BPQ為等邊三角形，請直接寫出此時直線AP的函數表達式．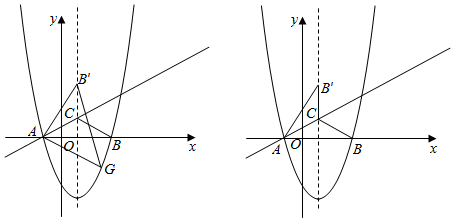
發布：2025/5/23 16:30:1組卷：1756引用：7難度：0.1 -
3．已知拋物線L：
經過點（-2，3）和（6，7），與x軸的交點為A、B，且點A在點B的左側，與y軸交于點C．y=12x2+bx+c
（1）求拋物線L的函數表達式；
（2）將拋物線L平移，得到拋物線L'，且點A經過平移后得到的對應點為A'．要使△A'BC是以BC為斜邊的等腰直角三角形，求滿足條件的拋物線L'的函數表達式．發布：2025/5/23 17:0:1組卷：417引用：2難度：0.1