 如圖,線段AB=6,C在線段AB的一個動點,以AC、BC為邊作等邊三角形△ACD和等邊三角形△BCE,⊙O外接△DCE,
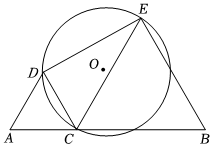
如圖,線段AB=6,C在線段AB的一個動點,以AC、BC為邊作等邊三角形△ACD和等邊三角形△BCE,⊙O外接△DCE,
(1)△DCE的外接圓的圓心是△DCE的 外心外心(外心或內心);點O的位置是否發生改變 不變不變(變或不變).
(2)若AC=x,△DCE為直角三角形時,求x的值.
(3)點O在△DCE的內部,直接寫出x的取值范圍.
(4)求⊙O半徑的最小值.
【考點】圓的綜合題.
【答案】外心;不變
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/31 1:0:2組卷:93引用:2難度:0.3
相似題
-
 1.如圖,在△ABC中,∠BAC=90°,點O在BC上,以線段OC的長為半徑的⊙O與AB相交于點D,分別交BC、AC于點E、F,連接ED并延長,交CA的延長線于點G.若∠DOC=2∠G,⊙O的半徑為3.
1.如圖,在△ABC中,∠BAC=90°,點O在BC上,以線段OC的長為半徑的⊙O與AB相交于點D,分別交BC、AC于點E、F,連接ED并延長,交CA的延長線于點G.若∠DOC=2∠G,⊙O的半徑為3.
(1)求證:AB是⊙O的切線.
(2)若BE=2,求AD的長.
(3)連接DF,當四邊形DOCF為菱形,求BE的長.發布:2025/6/1 7:30:2組卷:505引用:1難度:0.1 -
2.小明在學習了《圓周角定理及其推論》后,有這樣的學習體會:在Rt△ABC中,∠C=90°,當AB長度不變時,則點C在以AB為直徑的圓上運動(不與A、B重合).
[探索發現]
小明繼續探究,在Rt△ABC中,∠C=90°,AB長度不變.作∠A與∠B的角平分線交于點F,小明計算后發現∠AFB的度數為定值,小明猜想點F也在一個圓上運動.請你計算∠AFB的度數,并簡要說明小明猜想的圓的特征.
[拓展應用]
在[探索發現]的條件下,若AB=2,求出△AFB面積的最大值.3
[靈活運用]
在等邊△ABC中,AB=2,點D、點E分別在BC和AC邊上,且BD=CE,連接AD、BE交于點F,試求出△ABF周長的最大值.3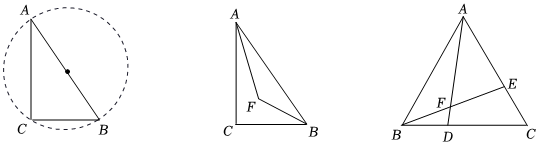 發布:2025/6/1 8:30:1組卷:588引用:1難度:0.2
發布:2025/6/1 8:30:1組卷:588引用:1難度:0.2 -
3.如圖1,點A在射線OP上,且OA=16,過點O在射線OP上方作射線OB,且
,點E從點A出發,沿AO方向以每秒2個單位長度的速度運動,同時點F從點O出發,沿OB方向以每秒1個單位長度的速度運動,當點E到達點O時,點E,F都停止運動.以點F為圓心,OF為半徑的半圓與射線OP交于點C,與射線OB交于點D,連接FC,DE,設運動時間為t秒(t>0).cos∠AOB=35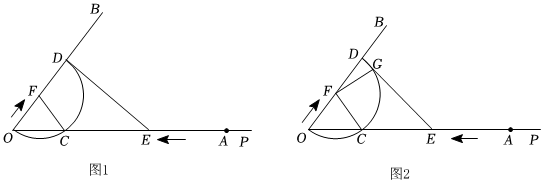
(1)用含t的式子表示OC的長為 ;當點E與點C重合時,OE的長為 ;
(2)若DE與半圓F相切,求OE的長;
(3)如圖2,當時,DE與半圓F的另一個交點為G,連接FG,求∠OED的度數及t=103的長;?CG
(4)若半圓F與線段DE只有一個公共點,直接寫出OE的取值范圍.發布:2025/6/1 8:30:1組卷:108引用:2難度:0.3


