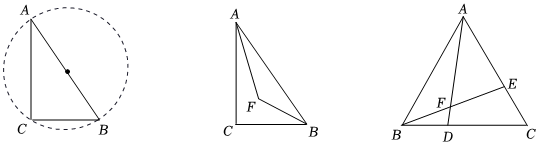
小明在學習了《圓周角定理及其推論》后，有這樣的學習體會：在Rt△ABC中，∠C=90°，當AB長度不變時，則點C在以AB為直徑的圓上運動（不與A、B重合）．
[探索發現]
小明繼續探究，在Rt△ABC中，∠C=90°，AB長度不變．作∠A與∠B的角平分線交于點F，小明計算后發現∠AFB的度數為定值，小明猜想點F也在一個圓上運動．請你計算∠AFB的度數，并簡要說明小明猜想的圓的特征．
[拓展應用]
在[探索發現]的條件下，若AB=23，求出△AFB面積的最大值．
[靈活運用]
在等邊△ABC中，AB=23，點D、點E分別在BC和AC邊上，且BD=CE，連接AD、BE交于點F，試求出△ABF周長的最大值．
3
3
【考點】圓的綜合題．
【答案】[探索發現]∠AFB=135°，F點在以AB為定弦，∠AFB為定角的圓上，
[拓展應用]3-3；
[靈活運用]4+2．
[拓展應用]3
2
[靈活運用]4+2
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 8:30:1組卷：588引用：1難度：0.2
相似題
-
1．如圖1，在⊙O中，OA=2，弦
，弓形AB是由AB=23和弦AB所圍成的圖形，弓形AB的高是?AB的中點到AB的距離，將弓形AB繞點B順時針旋轉α（0°≤α≤360°），點A的對應點為點A'，如圖2所示．?AB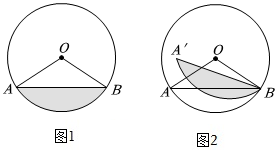
（1）分別求弓形AB的高和弓形AB的面積；
（2）當直線A'B與⊙O相切時，求α的度數并求此時點A'運動路徑的長度；
（3）當點O落在弓形AB（陰影部分，包括邊界）內時，請直接寫出α的取值范圍．發布：2025/6/1 22:30:2組卷：121引用：3難度：0.4 -
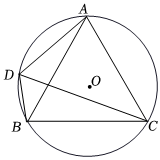2．如圖，⊙O為等邊△ABC的外接圓，半徑為3，點D在劣弧，上運動（不與點A，B重合），連接DA，DB，DC．?AB
（1）求證：DC是∠ADB的平分線；
（2）四邊形ADBC的面積S是線段DC的長x的函數嗎？如果是，求出函數解析式；如果不是，請說明理由；
（3）若點M，N分別在線段CA，CB上運動（不含端點），經過探究發現，點D運動到每一個確定的位置，△DMN的周長有最小值t,隨著點D的運動，t的值會發生變化，求所有t值中的最大值．發布：2025/6/2 9:30:1組卷：354引用：2難度：0.2 -
3．如圖1所示，在矩形OABC中，OA=
，OC=1，點D是射線OA上一動點，以OD為半徑作⊙O．2
（1）連接CD交⊙O于點E，連接OB，當DE的中點在OB上時，求OD的長；
（2）如圖2所示，當⊙O與AB邊相切時，設⊙O與BC交于點F，求劣弧的長；?AF
（3）連接AC，若⊙O與△ABC兩條邊同時相交，請直接寫出tan∠BCD的取值范圍．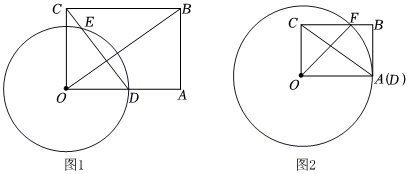
發布：2025/6/2 5:30:2組卷：93引用：3難度：0.4