課本呈現：如圖1，在射門游戲中，球員射中球門的難易程度與他所處的位置C對球門AB的張角（∠C）有關．當球員在C，D處射門時，則有張角∠C=∠D．某數學小組由此得到啟發，探究當球員在球門AB同側的直線l射門時的最大張角．
問題探究：（1）如圖2，小明探究發現，若過A、B兩點的動圓與直線l相交于點C、D，當球員在P處射門時，則有∠ACB＞∠APB．
小明證明過程如下：
設直線BP交圓于點E，連接AE，則∠ACB=∠AEB
∵∠AEB=∠APB∠APB+∠EAP
∴∠ACB=∠APB∠APB+∠EAP
∴∠ACB＞∠APB
（2）如圖3，小紅繼續探究發現，若過A、B兩點的動圓與直線l相切于點F，當球員在F處射門時，則有∠AFB＞∠ACB，你同意嗎？請你說明理由．
問題應用：如圖4，若∠BOC=45°，OB=102米，A是中點，球員在射線OC上的P點射門時的最大張角為45°，則OP的長度為 1010米．
問題遷移：如圖5，在射門游戲中球門AB=10，CD是球場邊線，DE=25，∠ADC是直角，EF⊥CD．若球員沿EF帶球前進，記足球所在的位置為點P，求∠APB的最大度數．（參考數據：sin67°≈1213，cos67°≈513，tan67°≈2.4，tan23°≈512，tan42°≈1213）
OB
=
10
2
sin
67
°≈
12
13
5
13
tan
23
°
≈
5
12
tan
42
°≈
12
13
【考點】圓的綜合題．
【答案】∠APB；∠APB；10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：915引用：3難度：0.5
相似題
-
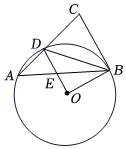1．如圖所示，△ABC的頂點A，B在⊙O上，頂點C在⊙O外，邊AC與⊙O相交于點D，∠BAC=45°，連接OB、OD，已知OD∥BC．
（1）求證：直線BC是⊙O的切線；
（2）若線段OD與線段AB相交于點E，連接BD．
①求證：△ABD∽△DBE；
②若AB?BE=6，求⊙O的半徑的長度．發布：2025/5/22 14:30:2組卷：1762引用：4難度：0.5 -
2．“同弧或等弧所對的圓周角相等”，利用這個推論可以解決很多數學問題．
（1）【知識理解】如圖1，圓O的內接四邊形ACBD中，∠ABC=60°，BC=AC，①∠BDC=；∠DAB ∠DCB（填“＞”，“=”，“＜”）；②將D點繞點B順時針旋轉60°得到點E，則線段DB，DC，DA的關系為 ；
（2）【知識應用】如圖2，AB是圓O的直徑，，猜想DA，DB，DC的數量關系，并證明；tan∠ABC=12
（3）【知識拓展】如圖3，已知AB=2，A，B分別是射線DM，DN上的兩個動點，以AB為邊往外構造等邊△ABC，點C在∠MDN內部，若∠D=120°，直接寫出四邊形ADBC面積S的取值范圍．
發布：2025/5/22 13:30:1組卷：234引用：1難度：0.2 -
3．已知△ABC內接于⊙O，AB是直徑，過點A作⊙O的切線MN．
（1）如圖1，求證：∠ABC=∠MAC；
（2）如圖2，當D是弧AC的中點時，過點D作DE⊥AB于E．求證：AC=2DE；
（3）如圖3，在（2）的條件下，DE與AC相交于點F，連接CD、BD與AC相交于點G，若△CDG的面積為12，EF=3，求點C到MN的距離．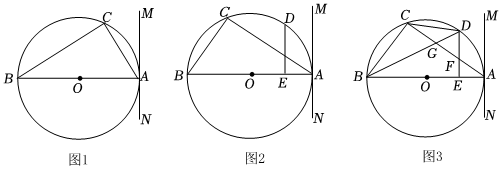
?發布：2025/5/22 14:0:1組卷：549引用：4難度：0.3