在△ABC中，∠ACB=90°，AC=BC，點D為AB的中點，M，N分別在BC，AC上，且BM=CN．
（1）求證：DM=DN；
（2）判斷△DMN的形狀，并說明理由．
【考點】全等三角形的判定與性質(zhì)；等腰直角三角形．
【答案】（1）證明見解析；
（2）△DMN是等腰直角三角形，理由見解析．
（2）△DMN是等腰直角三角形，理由見解析．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/10/22 11:0:1組卷：27引用：3難度：0.6
相似題
-
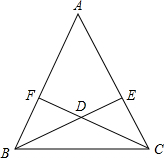1．已知：在△ABC中，BE⊥AC，CF⊥AB，且BE=CF，說明BD=CD的理由．發(fā)布：2025/5/28 8:30:1組卷：98引用：1難度：0.5 -
2．如圖，已知在△ABC中，∠BAC為直角，AB=AC，D為AC上一點，CE⊥BD于E．
（1）若BD平分∠ABC，求證CE=BD；12
（2）若D為AC上一動點，∠AED如何變化？若變化，求它的變化范圍；若不變，求出它的度數(shù)，并說明理由．發(fā)布：2025/5/28 7:30:2組卷：508引用：23難度：0.1 -
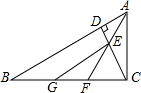3．如圖，在△ABC中，∠ACB=90°，CD⊥AB于D，AF平分∠BAC交CD于E，交BC于F，EG∥AB交BC于G，說明BG=CF的理由．發(fā)布：2025/5/28 7:30:2組卷：367引用：1難度：0.1