如圖，△ABC為等邊三角形，D為BC邊上一點，連接AD．
（1）如圖1，將AD繞點A順時針旋轉60°得到AE．連接DE，BE，若BEBD=710，BC=6，求CD的長度；
（2）如圖2，將AD繞點A順時針旋轉120°得到AE，連接CE交AB于F，G為AC邊的中點，連接FG，猜想FG與AE存在的關系，并證明你的猜想；
（3）如圖3，以AC為斜邊向AC邊右側作Rt△AEC，連接BE，F為BE上一點，且BF=35BE，連接DF，若AB=4，CD=1，當DF取最小值時，請直接寫出△BDF的面積．
BE
BD
=
7
10
3
5
【考點】幾何變換綜合題．
【答案】（1）；
（2）FG∥AE，FG=AE；
（3）．
42
17
（2）FG∥AE，FG=
1
2
（3）
63
3
-
18
21
70
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1098引用：1難度：0.1
相似題
-
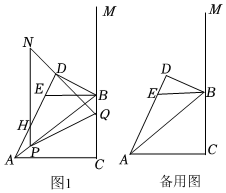1．如圖1，在Rt△ABC中，∠C=90°，AC=8，BC=6，BD平分△ABC的外角∠ABM，AD⊥BD于點D，過B點作BE∥AC交AD于點E．點P在線段AB上（不與端點A點重合），點Q在射線CB上，且CQ=2AP=2t,連結PQ，作P點關于直線BE的對稱點N，連結PN，NQ．
（1）求證：∠BAD=∠DBE．
（2）當Q在線段BC上時，PN與AD交于點H，若AH=EH，求HP的長．
（3）①當△PNQ的邊與△ABD的AD或BD邊平行時，求所有滿足條件的t的值．
②當點D在△PNQ內部時，請直接寫出滿足條件的t的取值范圍．發布：2025/5/25 18:30:1組卷：231引用：1難度：0.2 -
2．問題背景：
如圖，已知△ABC中，AB=AC=m,BC=n,∠BAC=α（0°＜α＜180°），點P為平面內不與點A，C重合的任意一點，連接CP，將線段CP繞點P順時針旋轉α，得線段PD，連接CD，AP．點E，F分別為BC，CD的中點，設直線AP與直線EF相交所成的較小角為β，探究的值AB和β的度數．EFAP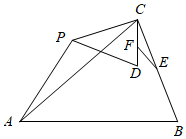
【問題發現】
（1）如圖1，α=60°時，=，β=；EFAP
（2）如圖2，α=90°時，=，β=．EFAP
【類比探究】
（3）如圖3，α=120°時，請探究出的值和β的度數并證明；EFAP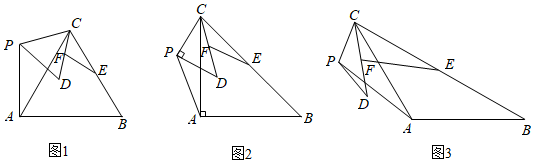
【拓展延伸】
（4）通過以上的探究請直接寫出你發現的規律：=（用含m、n的式子表示）；β=（用含α的式子表示）．EFAP發布：2025/5/25 18:30:1組卷：184引用：1難度：0.2 -
3．綜合與探究
問題情境
如圖，在矩形紙片ABCD中，點E．F分別是邊AD，BC上的動點，連接EF，BE，DF．將矩形紙片ABCD分別沿直線BE，DF折疊，點A的對應點為點M，點C的對應點為點N．
操作探究
（1）如圖（1），若點F與點M重合，DN與EF交于點G，求證：DG=GM；
探究發現
（2）如圖（2），當點M，N落在對角線BD上時，判斷并證明四邊形BFDE的形狀；
探究拓廣
（3）當點M，N落在對角線AC上時．
①在圖（3）中補全圖形；
②若AB=2，AD=3，求△BEF的面積．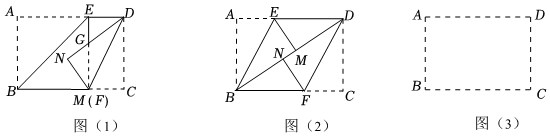
發布：2025/5/25 17:0:1組卷：557引用：2難度：0.4