問題背景：
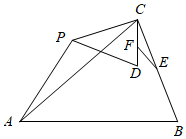
如圖，已知△ABC中，AB=AC=m,BC=n,∠BAC=α（0°＜α＜180°），點P為平面內不與點A，C重合的任意一點，連接CP，將線段CP繞點P順時針旋轉α，得線段PD，連接CD，AP．點E，F分別為BC，CD的中點，設直線AP與直線EF相交所成的較小角為β，探究EFAP的值AB和β的度數．
【問題發現】
（1）如圖1，α=60°時，EFAP=1212，β=60°60°；
（2）如圖2，α=90°時，EFAP=2222，β=45°45°．
【類比探究】
（3）如圖3，α=120°時，請探究出EFAP的值和β的度數并證明；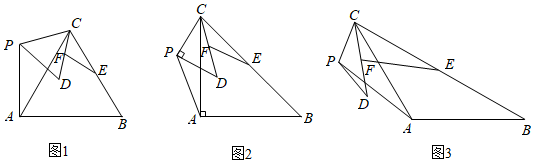
【拓展延伸】
（4）通過以上的探究請直接寫出你發現的規律：EFAP=n2mn2m（用含m、n的式子表示）；β=180°-α2180°-α2（用含α的式子表示）．
EF
AP
EF
AP
1
2
1
2
EF
AP
2
2
2
2
EF
AP
EF
AP
n
2
m
n
2
m
180
°
-
α
2
180
°
-
α
2
【考點】幾何變換綜合題．
【答案】；60°；；45°；；
1
2
2
2
n
2
m
180
°
-
α
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/25 18:30:1組卷：184引用：1難度：0.2
相似題
-
1．[問題發現]如圖1，在Rt△ABC中，∠BAC=90°，AB=AC，D為斜邊BC上一點（不與點B，C重合），將線段AD繞點A順時針旋轉90°得到AE，連接EC，則線段BD與CE的數量關系是 ，位置關系是 ；
[探究證明]如圖2，在Rt△ABC和Rt△ADE中，∠BAC=∠DAE=90°，AB=AC．AD=AE，將△ADE繞點A旋轉，當點C，D，E在同一條直線上時，BD與CE具有怎樣的位置關系，說明理由；
[拓展延伸]如圖3，在Rt△BCD中，∠BCD=90°，BC=2CD=4，過點C作CA⊥BD于A．將△ACD繞點A順時針旋轉，點C的對應點為點E．設旋轉角∠CAE為a（0°＜a＜360°），當C，D，E在同一條直線上時，畫出圖形，并求出線段BE的長度．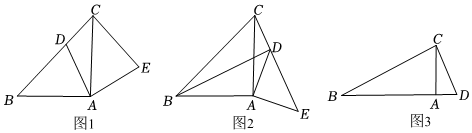
發布：2025/5/25 22:0:1組卷：405引用：1難度：0.3 -
2．【發現奧秘】
（1）如圖1，在等邊三角形ABC中，AB=2，點E是△ABC內一點，連接AE，EC，BE，分別將AC，EC繞點C順時針旋轉60°得到DC，FC，連接AD，DF，EF．當B，E，F，D四個點滿足 時，BE+AE+CE的值最小，最小值為 ．
【解法探索】
（2）如圖2，在△ABC中，∠ACB=90°，AC=BC，點P是△ABC內一點，連接PA，PB，PC，請求出當PA+PB+PC的值最小時∠BCP的度數，并直接寫出此時PA：PB：PC的值．（提示：分別將PC，AC繞點C順時針旋轉60°得到DC，EC，連接PD，DE，AE）
【拓展應用】
（3）在△ABC中，∠ACB=90°，∠BAC=30°，BC=2，點P是△ABC內一點，連接PA，PB，PC，直接寫出當PA+PB+PC的值最小時，PA：PB：PC的值．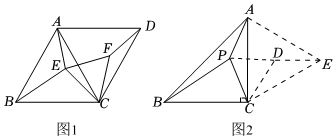
發布：2025/5/26 0:30:1組卷：232引用：1難度：0.4 -
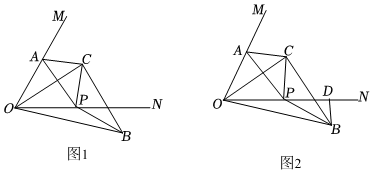3．下面是某數學興趣小組對一個數學問題作的探究活動：
（1）如圖1，小明同學得出△OAC≌△BPC，他的判斷理由是 ．問題：
如圖1，已知，∠MON=60°，點A在邊OM上，點P是邊ON上一動點，以線段AP為斜邊作Rt△ACP，AC=PC，∠ACP=90°（C和O在AP的兩側），連接OC，將線段OC繞C逆時針旋轉90°至BC，連接OB．
A．SSS
B．SAS
C．AAS
D．ASA
（2）如圖2，小穎同學作BD⊥ON于D，她認為OA與BD存在某種數量關系，那么OA與BD是否有數量關系？如果有數量關系，請你寫出OA與BD的數量關系并說明理由；
（3）如圖1，小華說，當OA=2，當△AOP是直角三角形時，可求出OB2的值，請你直接寫出OB2的值．發布：2025/5/25 22:30:2組卷：142引用：2難度：0.1