我校七年級數學興趣小組成員們自主開展數學微項目研究.結合本階段學內容特點,他們決定研究數的一些“神秘”性質.
| 探索數的神秘性質 | ||
| 素材 | 尼科馬霍斯是古希臘數學家,他的著作《算術入門》中記載了各種數分門別類的整理成果,其中任何一個整數m的立方都可以寫成m個連續奇數之和. | 舉例論證: 13=1;23=3+5;33=7+9+11; 請你按規律寫出: 43= 13+15+17+19 13+15+17+19 . |
| 規律總結 | 當m是奇數7時,則等號右邊式子中的中間數(即第4個數)為 49 49 ; |
當m為偶數10時,則等號右邊式子中的中間兩個數(即第5和第6個數)為 99,101 99,101 . |
| 綜合應用 | 利用上面結論計算:13+23+33+…+93+103+113. | |
| 拓展延伸 | 我們還發現以下規律:已知m≥2,n≥3,且m,n均為正整數,如果將mn進行如圖所示的“分解”: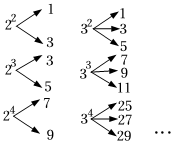 若mn(且m,n均為不大于7的正整數)的分解中有奇數31,則mn的值為 64或216 64或216 . |
|
【答案】13+15+17+19;49;99,101;64或216
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/7 9:0:8組卷:406引用:4難度:0.4
相似題
-
1.埃及同中國一樣,也是世界上著名的文明古國,古代埃及人處理分數與眾不同,他們一般只使用分子為1的分數,例如:用
+13來表示115,用25+14+17來表示128,等等.現在有90個埃及分數:37,12,13,14,…,15,190,你能從中挑出10個,加上正負號,使他們的和等于-1嗎?191發布:2025/6/16 13:30:1組卷:306引用:4難度:0.1 -
2.根據規律填代數式,
1+2=;1+2+3=2×(2+1)2;1+2+3+4=3×(3+1)2;1+2+3+…+n=.4×(4+1)2發布:2025/6/16 14:0:1組卷:227引用:4難度:0.9 -
3.觀察以下等式:
第1個等式:+12=1,第2個等式:11×2+13=12×3,第3個等式:12+14=13×4,第4個等式:13+15=14×5,第5個等式:14+16=15×6,…按照以上規律,解決下列問題:15
(1)寫出第6個等式:.
(2)寫出你猜想的第n個等式:(用含n的式子表示),并證明其正確性.發布:2025/6/16 14:0:1組卷:105引用:2難度:0.6


