綜合與實踐課上，老師與同學們以“等腰直角三角形”為主題開展數學活動．
（1）操作判斷 在△ABC中，∠ACB=90°，AC=BC，點D在AB上，以BC為邊，在△ABC外側作△BEC≌△ADC．①根據以上操作，如圖1，用尺規補出圖形（保留作圖痕跡，不寫畫法），并說明你的作圖中，兩個三角形全等的依據；
②此時∠ABE=9090度；
（2）遷移探究 在（1）的條件下，連接AE，△AEC和△BCD的面積是否相等？說明理由．
（3）拓展應用 如圖2，已知∠ABP=∠ACB=90°，AC=BC，點D在AB上，AB=42，∠BDC=120°，在射線BP上存在點E，使 S△ACE=S△BCD，請直接寫出相應的BE的長．
AB
=
4
2
【考點】三角形綜合題．
【答案】90
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：136引用：1難度：0.3
相似題
-
1．（1）如圖1，在△ABC中，點D為AC邊上一點，AD=
CD，連接BD，過點A作AE∥BC交BD的延長線于點E，若S△ABC=24，則S△ABE=；12
（2）如圖2，在△ABC中，AC=8，∠B=60°，求△ABC面積的最大值；
（3）公園作為城市生態環節的重要組成部分，從來都是衡量一座城市的生態底蘊和宜居指數的重要指標．西安高新區建區以來，始終堅持生態優先的綠色發展之路，高度重視公園、綠地建設，先后建成了新紀元公園、唐城墻遺址公園等一批綜合性公園．近年來，進入發展“快車道”的西安高新區，更是把公園建設當做提升區域生態環境和城市品質的重要任務，近期高新區管委會擬在一片空地上修建一座矩形城市公園ABCD，如圖3，按照規劃，在這個矩形公園里要修建一個三角形活動中心△AEC，點E在AD邊上，且DE：CD=1：，活動中心△AEC被景觀大道EF（寬度不計）分割為△AEF和△ECF兩塊區域，已知EF=200米，且S△AEF=3；求當△AEC面積最大時矩形ABCD的面積．13S△AEC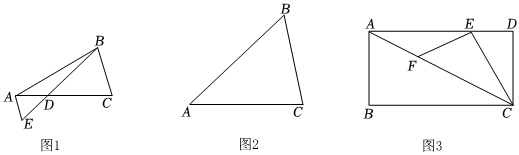
發布：2025/5/23 7:30:1組卷：487引用：1難度：0.1 -
2．在△ABC中，AB=AC，D為射線BC上一點，DB=DA，E為射線AD上一點，且AE=CD，連接BE．
（1）如圖1，若∠ADB=120°，，求DE的長；AC=3
（2）如圖2，若BE=2CD，連接CE并延長，交AB于點F，求證：CE=2EF；
（3）如圖3，若BE⊥AD，垂足為點E，猜想AE、AD、BE的數量關系，并證明．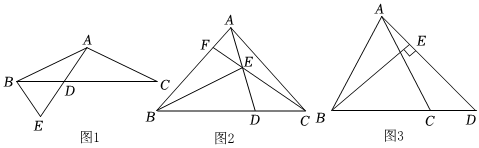
發布：2025/5/23 7:0:1組卷：203引用：1難度：0.1 -
3．（1）如圖，△AOB和△COD是等腰直角三角形，∠AOB=∠COD=90°，點C在OA上，點D在線段BO延長線上，連接AD，BC．線段AD與BC的數量關系為 ．
（2）如圖2，將圖1中的△COD繞點O順時針旋轉α（0°＜α＜90°）第一問的結論是否仍然成立；如果成立，證明你的結論，若不成立，說明理由．
（3）如圖3，若AB=8，點C是線段AB外一動點，，連接BC，若將CB繞點C逆時針旋轉90°得到CD，連接AD，則AD的最大值是 ．AC=33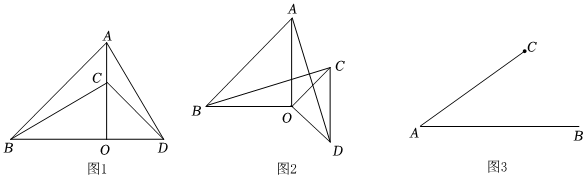
發布：2025/5/23 7:0:1組卷：274引用：4難度：0.3