如圖，在?ABCD中，AB=8，BC=4，∠B=60°，點E從點B出發沿BA向終點A運動，過點E作AB邊的垂線，交?ABCD其他邊于點F，在EF的右上方作正方形EFGH．
?
（1）如圖1，點F為BC中點時，求正方形EFGH的面積．
（2）如圖2，點E從B點運動到A點的過程中，點O為該正方形對角線FH的中點．
①設BE=x,△OCF的面積為y,求上述運動過程中y關于x的函數表達式．
②當△OCF有一個內角為30°時，求BE的長．
【考點】四邊形綜合題．
【答案】（1）3；
（2）y=
；
（3）x=8-4?或或5-或5+．
（2）y=
- 3 + 3 4 x 2 + 3 + 3 2 x （ 0 ＜ x ≤ 2 ） |
3 2 x - 3 （ 2 ＜ x ≤ 8 ） |
（3）x=8-4
3
32
-
8
3
13
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/18 8:0:9組卷：130引用：1難度：0.1
相似題
-
1．【了解概念】
定義提出：有一組鄰邊相等的凸四邊形叫做“等鄰邊四邊形”．
【理解運用】
（1）如圖1，在3×3的正方形網格中，每個小正方形的頂點稱為格點，每個小正方形的邊長均為1，線段AB、BC的端點均在格點上，在圖1的方格紙中畫出一個等鄰邊四邊形ABCD，要求：點D在格點上；
（2）如圖2，在等鄰邊四邊形ABCD中，AB=AD=4，∠A=60°，∠ABC=90°，，求CD的長；BC=33
【拓展提升】
（3）如圖3，在平面直角坐標系中，矩形OABC的頂點A、C分別在x、y軸正半軸上，已知OC=4，OA=6，D是OA的中點．在矩形OABC內或邊上，是否存在點E，使四邊形OCED為面積最大的“等鄰邊四邊形”，若存在，請求出四邊形OCED的最大面積及此時點E的坐標；若不存在，請說明理由．
發布：2025/5/23 5:30:3組卷：951引用：14難度：0.3 -
2．（1）感知：如圖①，四邊形ABCD和CEFG均為正方形，BE與DG的數量關系為 ；
（2）拓展：如圖②，四邊形ABCD和CEFG均為菱形，且∠A=∠F，請判斷BE與DG的數量關系，并說明理由；
（3）應用：如圖③，四邊形ABCD和CEFG均為菱形，點E在邊AD上，點G在AD延長線上．若AE=2ED，∠A=∠F，△EBC的面積為8，求菱形CEFG的面積．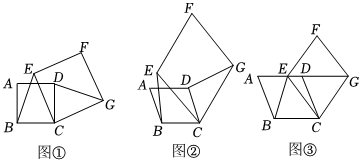
發布：2025/5/23 5:30:3組卷：229引用：1難度：0.3 -
3．如圖，在正方形ABCD中，，將正方形ABCD繞點C按順時針方向旋轉90°得到正方形CEFM．動點P從點A出發，沿AC方向運動，運動速度為1cm/s.過點P作AC的垂線，交AD于點Q，連接CQ，交PF于點H．設動點P的運動時間為t s（0＜t＜8）．解答下列問題：AB=42cm
?（1）當t為何值時，S△APQ：S△CDF=1：4？
（2）設△PFQ的面積為S cm2，求S與t之間的關系式；
（3）當運動時間為2 s時，求PH的長；
（4）若N是PF的中點，在運動的過程中，點N到∠DFE兩邊距離的和是否為定值？請說明理由．發布：2025/5/23 5:30:3組卷：264引用：1難度：0.1