某數學興趣小組在數學課外活動中，對多邊形內兩條互相垂直的線段做了如下探究：
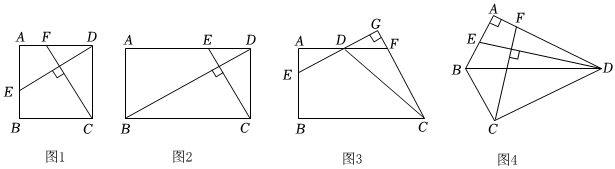
【觀察與猜想】（1）如圖1，在正方形ABCD中，點E，F分別是AB，AD上的兩點，連接DE，CF，DE⊥CF，則DECF的值為 11；
（2）如圖2，在矩形ABCD中，∠DBC=30°，點E是AD上的一點，連接CE，BD，且CE⊥BD，則CEBD的值為 3333；
【類比探究】（3）如圖3，在四邊形ABCD中，∠A=∠B=90°，點E為AB上一點，連接DE，過點C作DE的垂線交ED的延長線于點G，交AD的延長線于點F，求證：DE?AB=CF?AD；
【拓展延伸】（4）如圖4，在Rt△ABD中，∠BAD=90°，AB=4，AD=8，將△ABD沿BD翻折，點A落在點C處得△CBD，點E，F分別在邊AB，AD上，連接DE，CF，且DE⊥CF，求DECF的值．
DE
CF
CE
BD
3
3
3
3
DE
CF
【考點】相似形綜合題．
【答案】1；
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：935引用：2難度：0.3
相似題
-
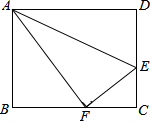1．在矩形ABCD中，E為DC邊上一點，把△ADE沿AE翻折，使點D恰好落在BC邊上的點F．
（1）求證：△ABF∽△FCE；
（2）若AB=2，AD=4，求EC的長；3
（3）若AE-DE=2EC，記∠BAF=α，∠FAE=β，求tanα+tanβ的值．發布：2025/5/31 9:0:2組卷：4163引用：5難度：0.1 -
2．閱讀下列材料，并完成相應任務：
幾何是數學的一個分支，幾何中有個對自然美體現非常完美的數值，叫黃金分割點．黃金分割被廣泛應用于建筑等領域．黃金分割指把一條線段分為兩部分，使其中較長部分與線段總長之比等于較短部分與較長部分之比，該比值為，用下面的方法（如圖①）就可以作出已知線段AB的黃金分割點H：5-12
①以線段AB為邊作正方形ABCD，
②取AD的中點E，連接EB，
③延長DA到F，使EF=EB，
④以線段AF為邊作正方形AFGH，點H就是線段AB的黃金分割點．
以下是證明點H就是線段AB的黃金分割點的部分過程：
證明：設正方形ABCD的邊長為1，則AB=AD=1，
∵E為AD中點，∴，AE=12
∴在Rt△BAE中，，BE=AB2+AE2=12+（12）2=52
∴，EF=BE=52
∴，…AF=EF-AE=5-12
問題：
（1）補全題中的證明過程；
（2）如圖②，點C為線段AB的黃金分割點（AC＞BC），分別以AC、BC為邊在線段AB同側作正方形ACDE和矩形CBFD，連接BD、BE．求證：△EAB∽△BCD；
（3）如圖③，在正五邊形ABCDE中，對角線AD、AC與EB分別交于點M、N，其中就包含有多個黃金分割點．如果AE=1，則AM的長度為 ，AD的長度為 ．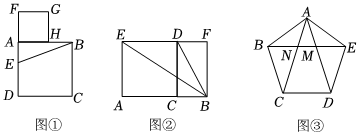
發布：2025/5/31 15:30:1組卷：150引用：1難度：0.1 -
3．如圖，已知矩形ABCD中，E是邊AD上一點，將△BDE沿BE折疊得到△BFE，連接DF．
（1）如圖1，BF落在直線BA上時，求證△DFA∽△BEA；
（2）如圖2，當時，BF與邊AD相交時，在BE上取一點G，使∠BAG=∠DAF，AG與BF交于點H，ADAB=2
①求的值；AFAG
②當E是AD的中點時，若FD?FH=18，求AG的長．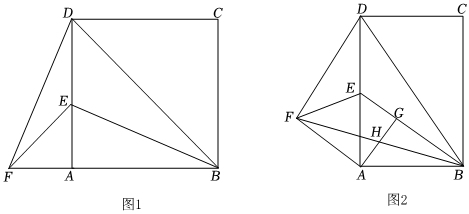
發布：2025/5/31 11:0:1組卷：631引用：3難度：0.1