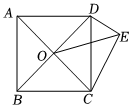
如圖，四邊形ABCD為正方形，O為AC、BD的交點，△DCE為直角三角形，∠CED=90°，∠DCE=30°，若正方形的邊長為2，則OE的長為 6+226+22．
6
+
2
2
6
+
2
2
【考點】正方形的性質；含30度角的直角三角形．
【答案】
6
+
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/2 8:30:1組卷：109引用：1難度：0.3
相似題
-
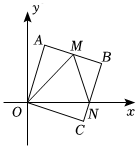1．如圖，在平面直角坐標系xOy中，四邊形OABC是正方形，點M，N分別是邊AB，BC上的點，已知點A（1，3），點N（n,0），∠MON=45°，連接MN，則△MNB的周長為 ．發布：2025/6/4 2:0:5組卷：947引用：5難度：0.3 -
2．菱形ABCD的對角線AC=6，BD=4，以AC為邊作正方形ACEF，則BF的長為（ ）
發布：2025/6/4 4:30:1組卷：55引用：2難度：0.4 -
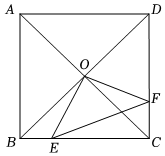3．已知：如圖，正方形ABCD中，AB=2，AC，BD相交于點O，E，F分別為邊BC，CD上的動點（點E，F不與線段BC，CD的端點重合）且BE=CF，連接OE，OF，EF．在點E，F運動的過程中，有下列四個結論：
①△OEF始終是等腰直角三角形；
②△OEF面積的最小值是1；
③至少存在一個△ECF，使得△ECF的周長是2+；3
④四邊形OECF的面積始終是1．
所有正確結論的序號是（ ）發布：2025/6/4 2:30:1組卷：421引用：3難度：0.6