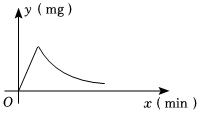
為預防傳染病，某校定期對教室進行“藥熏消毒”．已知某種藥物在燃燒階段，室內每立方米空氣中的含藥量y（mg）與燃燒時間x（min）成正比例；一次性燃燒完以后，y與x成反比例（如圖所示）．在藥物燃燒階段，實驗測得在燃燒5分鐘后，此時教室內每立方米空氣含藥量為72mg.
（1）若一次性燃燒完藥物需10分鐘．
①分別求出藥物燃燒時及一次性燃燒完以后y關于x的函數表達式．
②當每立方米空氣中的含藥量低于75mg時，對人體方能無毒害作用，那么從消毒開始，在哪個時間段學生不能停留在教室里？
（2）已知室內每立方米空氣中的含藥量不低于0.7mg時，才能有效消毒，如果有效消毒時間要持續120分鐘，問要一次性燃燒完這種藥物需多長時間？
7
2
7
5
【考點】反比例函數的應用．
【答案】（1）①y=x（0≤x≤10）；y=（x≥10）；
②當2≤x≤50時，學生不能在教室停留；
（2）要一次性燃燒完這種藥物需11分鐘．
7
10
70
x
②當2≤x≤50時，學生不能在教室停留；
（2）要一次性燃燒完這種藥物需11分鐘．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/11 8:0:9組卷：909引用：1難度：0.5
相似題
-
1．某物體質量一定，若體積V=40m3，則密度ρ=1.6kg/m3．
（1）寫出此物體的密度ρ與體積V的函數關系式，并畫出它的圖象；
（2）當物體密度ρ=3.2kg/m3時，它的體積V是多少？
（3）若讓該物體的體積控制在4m3～80m3之間，則該物體的密度是如何變化的？發布：2025/6/22 18:0:1組卷：40引用：4難度：0.7 -
2．喝綠茶前需要燒水和泡茶兩個工序，即需要將電熱水壺中的水燒到100℃，然后停止燒水，等水溫降低到適合的溫度時再泡茶，燒水時水溫y（℃）與時間x（min）成一次函數關系；停止加熱過了1分鐘后，水壺中水的溫度y（℃）與時間x（min）近似于反比例函數關系（如圖）．已知水壺中水的初始溫度是20℃，降溫過程中水溫不低于20℃．
（1）分別求出圖中所對應的函數關系式，并且寫出自變量x的取值范圍；
（2）從水壺中的水燒開（100℃）降到80℃就可以進行泡制綠茶，問從水燒開到泡茶需要等待多長時間？發布：2025/6/22 20:0:1組卷：1392引用：15難度：0.7 -
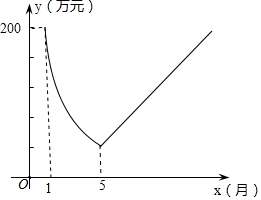3．保護生態環境，建設綠色社會已經從理念變為人們的行動．某化工廠2009年1月的利潤為200萬元．設2009年1月為第1個月，第x個月的利潤為y萬元．由于排污超標，該廠從2009年1月底起適當限產，并投入資金進行治污改造，導致月利潤明顯下降，從1月到5月，y與x成反比例．到5月底，治污改造工程順利完工，從這時起，該廠每月的利潤比前一個月增加20萬元（如圖）
（1）分別求該化工廠治污期間及治污改造工程完工后y與x之間對應的函數關系式．
（2）治污改造工程完工后經過幾個月，該廠利潤才能達到2009年1月的水平？
（3）當月利潤少于100萬元時為該廠資金緊張期，問該廠資金緊張期共有幾個月？發布：2025/6/23 15:30:2組卷：1495引用：12難度：0.5